
分析 (1)根据绝对值的意义得到|a+2|=4,求出a的值即可;(2)由|x+a|≤1在[-1,0]恒成立得到(-1-x)max≤a≤(1-x)min,求出a的范围即可.
解答 解:(1)∵f(x)=|x-2|+|x+a|≥|(x-2)-(x+a)|=|a+2|,
当且仅当(x-2)(x+a)≤0时取等号,
∴f(x)min=|a+2|,
由|a+2|=4,解得:a=2或a=-6;
(2)原命题等价于|x+a|+2-x≤3-x在[-1,0]恒成立,
即|x+a|≤1在[-1,0]恒成立,
即-1-x≤a≤1-x在[-1,0]恒成立,
即(-1-x)max≤a≤(1-x)min,
故a∈[0,1].
点评 本题考查了解绝对值不等式问题,考查绝对值的性质以及转化思想,是一道中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 变量x | 2.7 | 2.9 | 3 | 3.2 | 4.2 |
| 变量y | 46 | 49 | m | 53 | 55 |
| A. | 50 | B. | 51 | C. | 52 | D. | 53 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
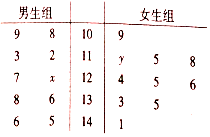 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com