
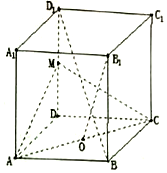
 在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.
在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.分析 (1)利用线面垂直的判定定理证明能证明B1O⊥平面ACM.
(2)由${V}_{O-A{B}_{1}M}$=${V}_{A-O{B}_{1}M}$,利用锥体的体积公式求出三棱锥O-AB1M的体积.
解答 证明:(1)∵AC⊥BD,DD1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD1,且BD∩DD1=D,
∴AC⊥平面BDD1B1,
OB1?平面BDD1B1,∴B1O⊥AC,
连结B1M,在△B1MO中,$M{O}^{2}={1}^{2}+(\sqrt{2})^{2}$=3,
${B}_{1}{O}^{2}={2}^{2}+(\sqrt{2})^{2}=6$,${B}_{1}{M}^{2}={1}^{2}+(2\sqrt{2})^{2}=9$,
∴${B}_{1}{M}^{2}=M{O}^{2}+{B}_{1}{O}^{2}$,
∴B1O⊥OM…(10分)
又OM∩AC=O,∴B1O⊥平面AMC.
解:(2)∵正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,
∴AC⊥BD,AC⊥DM,
∵BD∩DM=D,∴AO⊥平面OB1M,
∴三棱锥O-AB1M的体积:
${V}_{O-A{B}_{1}M}$=${V}_{A-O{B}_{1}M}$=$\frac{1}{3}×AO×{S}_{△O{B}_{1}M}$=$\frac{1}{3}×\frac{\sqrt{2}}{2}×\frac{1}{2}×\frac{\sqrt{6}}{2}×\frac{\sqrt{3}}{2}$=$\frac{1}{8}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 未服用药 | a | b | 40 |
| 服用药 | 5 | d | M |
| 总计 | 25 | N | 80 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3i}{25}$ | B. | -$\frac{3}{25}$ | C. | $\frac{3}{25}$ | D. | -$\frac{4}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (1,3) | C. | (2,3] | D. | (-∞,-2]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com