
���� ��1���������ַ��̵�ת������������C1����ͨ���̣�����C1�ķ��̻�Ϊ�����귽�̣�
��2������C1��C2�Ĺ�����ļ��������㷽����$\left\{\begin{array}{l}{��^2}-2��cos��+1-{a^2}=0\\ ��=2sin��\end{array}\right.$�����ѡ�0���ɷ������4sin2��-4sin��cos��+1-a2=0������֪$��=\frac{��}{4}$��������a��ֵ��
��� �⣺��1����ȥ����t�õ�C1����ͨ���̣�x-1��2+y2=a2����x=��cos�ȣ�y=sin�ȴ���C1����ͨ���̣��õ�C1�ļ����귽�̣���2-2��cos��+1-a2=0��
��2������C1��C2�Ĺ�����ļ��������㷽����$\left\{\begin{array}{l}{��^2}-2��cos��+1-{a^2}=0\\ ��=2sin��\end{array}\right.$�����ѡ�0��
�ɷ������4sin2��-4sin��cos��+1-a2=0������֪$��=\frac{��}{4}$���ɽ��1-a2=0��
����a��0���õ�a=1����a=1ʱ������ҲΪC1��C2�Ĺ����㶼��C3�ϣ�����a=1��
���� ���⿼�˲������̺ͼ����귽�̵�Ӧ�ã������˼�������ֱ������Ļ������ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��10�� | B�� | ��-1��2�� | C�� | ��0��1�� | D�� | ��1��10�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��6�� | B�� | ��-�ޣ�-6���ȣ�2��+�ޣ� | C�� | ��-�ޣ�-2���ȣ�6��+�ޣ� | D�� | ��-6��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 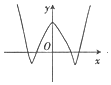 | C�� |  | D�� | 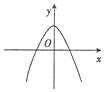 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
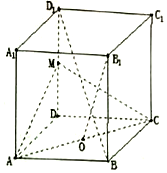 ��������ABCD-A1B1C1D1�У�MΪDD1���е㣬OΪAC���е㣬AB=1��
��������ABCD-A1B1C1D1�У�MΪDD1���е㣬OΪAC���е㣬AB=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 3 | C�� | -1 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ַDZ�Ҫ | B�� | ��Ҫ�dz�� | ||
| C�� | ��ֱ�Ҫ | D�� | �ȷdz���ַDZ�Ҫ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com