
分析 (1)可先选后排,共有C53C42A55种方法,计算即可.
(2)先选后排,共有C53C42A33A22种方法,计算即可.
(3)先选后排,共有C53C42C32A22A33种方法,计算即可.
解答 解:(1)从1,3,5,7,9中任取3个数字有C53种方法,
从2,4,6,8中任取2个数字有C42种方法,
再把取出的5个数全排列共有C53C42A55=7200
故一共可以组成7200个没有重复数字的五位数.
(2)从1,3,5,7,9中任取3个数字有C53种方法,
从2,4,6,8中任取2个数字有C42种方法,
先排万位、百位和个位有A33种,再排千位和十位有A22种,共有C53C42A33A22=720
故一共可以组成万位、百位和个位数字是奇数的无重复数字的五位数720个.
(3)从1,3,5,7,9中任取3个数字有C53种方法,
从2,4,6,8中任取2个数字有C42种方法,
由三个奇数选两个有C32种,再排千位和十位有A22种,剩下的三个数全排,有A33种,共有C53C42C32A22A33=2160
故一共可以组成千位和十位数字是奇数的无重复数字的五位数2160个.
点评 本题考查排列组合及简单的计数问题,先选后排是解决问题的关键,属中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知过点P(4,3)的光线,经x轴上一点A反射后的射线l过点Q(0,5).
如图,已知过点P(4,3)的光线,经x轴上一点A反射后的射线l过点Q(0,5).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
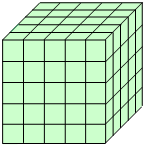 如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )
如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,则取到含油漆的概率为( )| A. | $\frac{12}{125}$ | B. | $\frac{27}{125}$ | C. | $\frac{98}{125}$ | D. | $\frac{168}{125}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
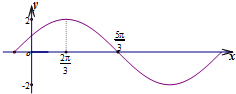
| A. | ω=1,φ=$\frac{π}{3}$ | B. | ω=1,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com