
分析 由题意可得,θ的终边在第一象限,或角θ的终边在第三象限.利用任意角的三角函数的定义,分类讨论,求得sinθ,cosθ,tanθ的值.
解答 解:根据角θ的终边在直线y=2x上,可得角θ的终边在第一象限,或角θ的终边在第三象限.
当角θ的终边在第一象限时,在它的终边上任意取一点P(1,2),则x=1,y=2,r=|OP|=$\sqrt{5}$,
此时,cosθ=$\frac{\sqrt{5}}{5}$,sinθ=$\frac{2\sqrt{5}}{5}$,tanθ=2.
当角θ的终边在第三象限时,在它的终边上任意取一点P(-1,-2),则x=-1,y=-2,r=|OP|=$\sqrt{5}$,
此时,cosθ=-$\frac{\sqrt{5}}{5}$,sinθ=$\frac{2\sqrt{5}}{5}$-,tanθ=2.
点评 本题主要考查任意角的三角函数的定义,体现了分类讨论的数学思想,属于基础题.


科目:高中数学 来源: 题型:解答题
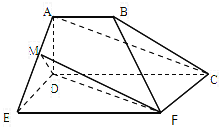 如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
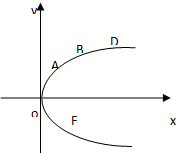 设A(x1,y1),B(x2,y2),D(x3,y3)是抛物线y2=4x上三点,F是抛物线的焦点且|AF|,|BF|,|DF|成等差数列.当AD的垂直平分线与x轴交于点T(3,0)时,求点B的坐标.
设A(x1,y1),B(x2,y2),D(x3,y3)是抛物线y2=4x上三点,F是抛物线的焦点且|AF|,|BF|,|DF|成等差数列.当AD的垂直平分线与x轴交于点T(3,0)时,求点B的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com