
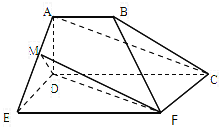
 如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.分析 (1)当M是线段AE的中点时,连结CE交DF于N,连结MN,则MN∥AC,由此得到AC∥平面MDF.
(2)将几何体ADE-BCF补成三棱柱ADE-B'CF,由此利用割补法能求出空间几何体M-DEF与空间几何体ADM-BCF的体积之比.
解答 解:(1)当M是线段AE的中点时,AC∥平面MDF,证明如下:(1分)
连结CE交DF于N,连结MN,由于M、N分别是AE、CE的中点,
所以MN∥AC,又MN在平面MDF内,(4分)
所以AC∥平面MDF (6分)
(2)将几何体ADE-BCF补成三棱柱ADE-B'CF,
三棱柱ADE-B'CF的体积为V=S△ADE•CD=$\frac{1}{2}$×2×2×4=8(8分)
则几何体ADE-BCF的体积:
VADE-BCF=V三棱柱ADE-ECF-V${\;}_{F-B{B}^{‘}C}$=8-$\frac{1}{3}×(\frac{1}{2}×2×2)×2=\frac{20}{3}$(10分)
又三棱锥F-DEM的体积V三棱锥F-DEM=$\frac{1}{3}×(\frac{1}{2}×2×4)×1=\frac{4}{3}$,(11分)
∴空间几何体M-DEF与空间几何体ADM-BCF的体积之比为:$\frac{4}{3}$:($\frac{20}{3}-\frac{4}{3}$)=$\frac{1}{4}$(12分)
点评 本题考查满足线面垂直的点的位置的确定,考查两个几何体的体积之比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | A?B | C. | A∩B=A | D. | A∩B={x|1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,7)∪{-4e-2,0} | B. | [3,7)∪{-4e-2} | C. | [4e-2,7) | D. | [0,7]∪{-4e-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com