练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
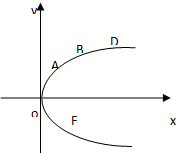
    6．设A（x1，y1），B（x2，y2），D（x3，y3）是抛物线y2=4x上三点，F是抛物线的焦点且|AF|，|BF|，|DF|成等差数列．当AD的垂直平分线与x轴交于点T（3，0）时，求点B的坐标．

    分析 由|AF|，|BF|，|DF|成等差数列，则2|BF|=|AF|+|DF|，即，从而问题可解．

    解答 解：由|AF|，|BF|，|DF|成等差数列，则2|BF|=|AF|+|DF|，即2x2=x1+x3
    直线AD斜率k=$\frac{{y}_{3}-{y}_{1}}{{x}_{3}-{x}_{1}}$=$\frac{4}{{y}_{3}+{y}_{1}}$．
    所以y1+y3=$\frac{4}{k}$，设AD中点为（x2，$\frac{2}{k}$）
    故AD的垂直平分线为y-$\frac{2}{k}$=-$\frac{1}{k}$（x-x2）
    令y=0，得x=2+x2，∴x2=1，代入y2=4x得y=±2，故B（1，2）或B（1，-2）．

    点评 本题考查了抛物线的简单几何性质，考查了抛物线的方程，体现了整体运算思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．抛物线Γ：y2=16x的焦点F，斜率为k的直线l与抛物线Γ交于M、N两点，若线段MN的垂直平分线的横截距为a（a＞0），n=|MF|+|NF|，则2a-n=8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设函数$f（x）=cos（2x+\frac{π}{3}）+\sqrt{3}sin2x+2m，（x∈R，m∈R）$，
    （Ⅰ）求函数f（x）的最小正周期及单调增区间；
    （Ⅱ）当$0≤x≤\frac{π}{4}$时，f（x）的最小值为0，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右两焦点分别为F1，F2，点P在椭圆上，正三角形△POF2面积为$\sqrt{3}$，则椭圆的方程为$\frac{x^2}{{2\sqrt{3}+4}}+\frac{y^2}{{2\sqrt{3}}}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知θ的顶角与原点重合，始边与x轴正半轴重合，终边y=2x上，求sinθ，cosθ，tanθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知a∈R，若$\frac{1+ai}{2+i}$为实数，则a=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设f（x）=$\frac{4}{{4}^{x}+2}$，Sn为数列{an}的前n项和，{an}满足a1=0，n≥2时，an=f（$\frac{1}{n}$）+f（$\frac{2}{n}$）+f（$\frac{3}{n}$）+…+f（$\frac{n-1}{n}$），则$\frac{{a}_{n+1}}{2{S}_{n}+{a}_{6}}$的最大值为$\frac{2}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若关于x的方程8x2-（m-1）x+m-7=0的两根均大于1，则m的取值范围是[25，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．将二进制数11101（2）转化为四进制数，正确的是（　　）
    A．120（4）B．131（4）C．200（4）D．202（4）

    查看答案和解析>>

    同步练习册答案