
【题目】设函数f(x)= ![]() x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
x2+ax﹣lnx(a∈R). (Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)当a>1时,讨论函数f(x)的单调性;
(Ⅲ)若对任意a∈(3,4)及任意x1 , x2∈[1,2],恒有 ![]() m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
m+ln2>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
【答案】解:(Ⅰ)函数的定义域为(0,+∞) 当a=1时,f(x)=x﹣lnx,则f′(x)= ![]()
令f′(x)>0,可得x<0或x>1,∵x>0,∴x>1;
令f′(x)<0,可得0<x<1,∵x>0,∴0<x<1;
∴x=1时,函数f(x)取得极小值为1;
(Ⅱ)f′(x)= 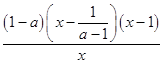
当 ![]() ,即a=2时,
,即a=2时, ![]() ,f(x)在(0,+∞)上是减函数;
,f(x)在(0,+∞)上是减函数;
当 ![]() ,即a>2时,令f′(x)<0,得
,即a>2时,令f′(x)<0,得 ![]() 或x>1;令f′(x)>0,得
或x>1;令f′(x)>0,得 ![]()
当 ![]() ,即1<a<2时,令f′(x)<0,得0<x<1或x>
,即1<a<2时,令f′(x)<0,得0<x<1或x> ![]() ;令f′(x)>0,得
;令f′(x)>0,得 ![]()
综上,当a=2时,f(x)在定义域上是减函数;
当a>2时,f(x)在(0, ![]() )和(1,+∞)上单调递减,在(
)和(1,+∞)上单调递减,在( ![]() ,1)上单调递增;
,1)上单调递增;
当1<a<2时,f(x)在(0,1)和( ![]() ,+∞)上单调递减,在(1,
,+∞)上单调递减,在(1, ![]() )上单调递增;
)上单调递增;
(Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减
∴当x=1时,f(x)有最大值,当x=2时,f(x)有最小值
∴ ![]()
∴对任意a∈(3,4),恒有 ![]()
∴m> ![]()
构造函数 ![]() ,则
,则 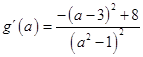
∵a∈(3,4),∴ 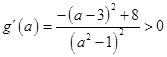
∴函数 ![]() 在(3,4)上单调增
在(3,4)上单调增
∴g(a)∈(0, ![]() )
)
∴m≥ ![]() .
.
【解析】(Ⅰ)确定函数的定义域,利用导数的正负,确定函数的单调性,从而可求函数的极值;(Ⅱ)求导函数f′(x)= ![]() ,分类讨论,利用导数的正负,确定函数的单调性; (Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减,从而可得
,分类讨论,利用导数的正负,确定函数的单调性; (Ⅲ)由(Ⅱ)知,当a∈(3,4)时,f(x)在[1,2]上单调递减,从而可得 ![]() 对任意a∈(3,4),恒有
对任意a∈(3,4),恒有 ![]() ,等价于m>
,等价于m> ![]() ,求出右边函数的值域,即可求得结论.
,求出右边函数的值域,即可求得结论.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
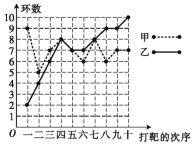
填写下表,请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 ,(
,(![]() 为参数),圆
为参数),圆![]() 的标准方程为
的标准方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与的交点为
与的交点为![]() ,与圆
,与圆![]() 的交点为
的交点为![]() ,且点
,且点![]() 恰好为线段
恰好为线段![]() 的中点,求
的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
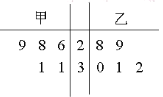
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的标号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=a﹣x2( ![]() ≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
A.[1, ![]() +2]
+2]
B.[1,e2﹣2]
C.[ ![]() +2,e2﹣2]
+2,e2﹣2]
D.[e2﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值;
的值;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() ,纵坐标压缩为原来的
,纵坐标压缩为原来的![]() ,得到曲线
,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com