
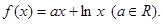
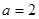 ,求曲线
,求曲线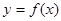 在
在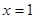 处的切线方程;
处的切线方程;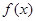 的单调区间;
的单调区间;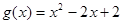 ,若对任意
,若对任意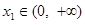 ,均存在
,均存在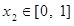 ,使得
,使得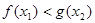 ,求
,求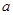 的取值范围.
的取值范围.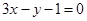 (2)详见解析(3)
(2)详见解析(3)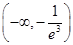
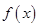 的解析式,把切点的横坐标带入函数
的解析式,把切点的横坐标带入函数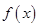 即可求出切点的纵坐标,对
即可求出切点的纵坐标,对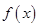 求导得到函数
求导得到函数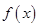 的导函数
的导函数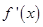 ,把
,把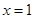 带入导函数
带入导函数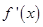 即可求的切线的斜率,利用点斜式即可得到切线的方程.
即可求的切线的斜率,利用点斜式即可得到切线的方程.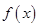 进行求导和求定义域,导函数
进行求导和求定义域,导函数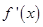 喊参数
喊参数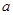 ,把
,把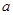 分为两种情况进行讨论,首先
分为两种情况进行讨论,首先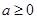 时,结合
时,结合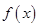 的定义域
的定义域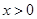 即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当
即可得到导函数在定义域内恒大于0,进而得到原函数在定义域内单调递增,当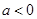 时,求解导函数
时,求解导函数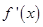 大于0和小于0的解集,得到原函数的单调递增和单调递减区间.
大于0和小于0的解集,得到原函数的单调递增和单调递减区间.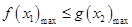 ,而
,而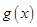 的最大值可以利用二次函数
的最大值可以利用二次函数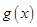 的图像得到函数
的图像得到函数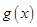 在区间
在区间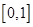 上的最值,函数
上的最值,函数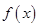 的最大值可以利用第二问的单调性求的,当
的最大值可以利用第二问的单调性求的,当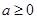 时,函数
时,函数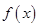 单调递增,无最大值,故不符合题意,当
单调递增,无最大值,故不符合题意,当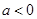 时,函数
时,函数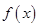 在
在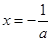 处前的最大值,带入不等式即可求的
处前的最大值,带入不等式即可求的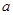 的取值范围.
的取值范围. , 1分
, 1分 ,所以斜率
,所以斜率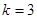 , 2分
, 2分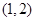 ,所以切线方程为
,所以切线方程为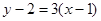 ),即
),即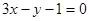
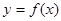 在
在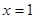 处切线的切线方程为
处切线的切线方程为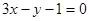 。 3分
。 3分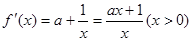 4分
4分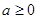 时,由于
时,由于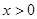 ,故
,故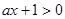 ,
,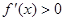 ,所以
,所以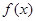 的单调递增区间为
的单调递增区间为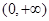 .
.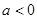 时,由
时,由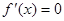 ,得
,得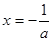 . 6分
. 6分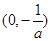 上,
上,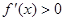 ,在区间
,在区间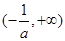 上,
上,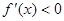 ,
,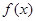 的单调递增区间为
的单调递增区间为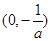 ,单调递减区间为
,单调递减区间为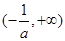 . 7分
. 7分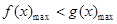 . 8分
. 8分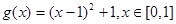 ,所以
,所以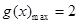 9分
9分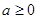 时,
时,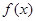 在
在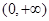 上单调递增,值域为
上单调递增,值域为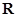 ,故不符合题意.
,故不符合题意.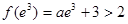 ,故不符合题意.) 10分
,故不符合题意.) 10分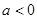 时,
时,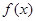 在
在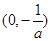 上单调递增,在
上单调递增,在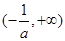 上单调递减,
上单调递减,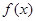 的极大值即为最大值,
的极大值即为最大值,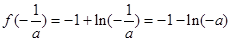 , 12分
, 12分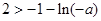 ,解得
,解得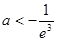 . 14分
. 14分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com