
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 由于(1+x)(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项,可知:(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项与含$\frac{1}{x}$的项,利用(x+$\frac{1}{{x}^{2}}$)n的展开式中的通项公式即可得出.
解答 解:∵(1+x)(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项,∴(x+$\frac{1}{{x}^{2}}$)n的展开式中没有常数项与含$\frac{1}{x}$的项,
(x+$\frac{1}{{x}^{2}}$)n的展开式中的通项公式:Tr+1=${∁}_{n}^{r}$xn-r$(\frac{1}{{x}^{2}})^{r}$=${∁}_{n}^{r}$xn-3r,(r=0,1,2,…,n).
经过验证:只有取n=10时,10-3r≠0,-1.
因此n的值可能是10.
故选:B.
点评 本题考查了二项式定理展开式的通项公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 对任意的x∈R,都有2x≥x2成立 | |
| B. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>x0 | |
| C. | 存在常数C,当x>C时,都有2x≥x2成立 | |
| D. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>2${\;}^{{x}_{0}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -log20162015 | B. | -1 | C. | (log20162015)-1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
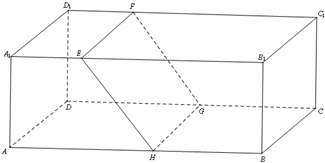 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极小值,无极大值 | B. | 有极大值,无极小值 | ||
| C. | 既有极小值,也有极大值 | D. | 既无极小值,也无极大值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com