
如图(1),等腰直角三角形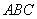 的底边
的底边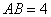 ,点
,点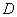 在线段
在线段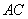 上,
上,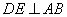 于
于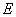 ,现将
,现将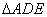 沿
沿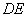 折起到
折起到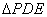 的位置(如图(2)).
的位置(如图(2)).
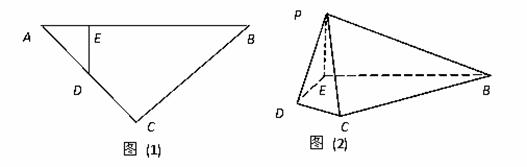
(Ⅰ)求证: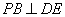 ;
;
(Ⅱ)若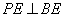 ,直线
,直线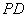 与平面
与平面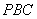 所成的角为
所成的角为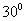 ,求
,求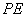 长.
长.
科目:高中数学 来源: 题型:
某学校实施“十二五高中课程改革”计划,高三理科班学生的化学与物理水平测试的成绩抽样统计如下表.成绩分A(优秀)、B(良好)、C(及格)三种等级,设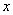 、
、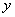 分别表示化学、物理成绩. 例如:表中化学成绩为B等级的共有20+18+4=42人.已知
分别表示化学、物理成绩. 例如:表中化学成绩为B等级的共有20+18+4=42人.已知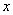 与
与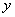 均为B等级的概率为0.18.
均为B等级的概率为0.18.
(1)求抽取的学生人数;
(2)若在该样本中,化学成绩的优秀率是0.3,
求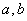 的值;
的值;
(3)物理成绩为C等级的学生中,已知
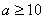 ,
,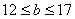 , 随机变量
, 随机变量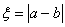 ,求
,求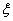 的
的
分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数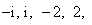 其中
其中 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件 “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率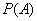 与事件
与事件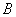 “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率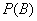 ;
;
(2)在两次试验中,记两次得到的数分别为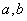 ,求随机变量
,求随机变量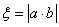 的分布列与数学期望
的分布列与数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com