
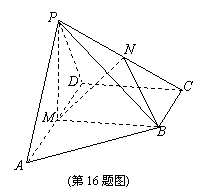
如图,在四棱锥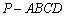 中,底面
中,底面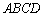 为直角梯形,
为直角梯形,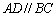 ,
,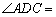 90°,
90°,
 ,
,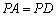 ,
,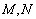 分别为
分别为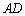 和
和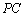 的中点.
的中点.
(1)求证: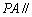 平面
平面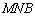 ;
;
(2)求证:平面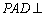 平面
平面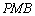 .
.
 |
科目:高中数学 来源: 题型:
已知函数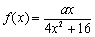 ,
,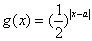 ,其中a∈R.
,其中a∈R.
(1)若0<a≤2,试判断函数h(x)=f (x)+g (x) 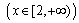 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)设函数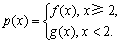 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得p (x1) = p (x2) 成立,试确定实数a的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得p (x1) = p (x2) 成立,试确定实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务。已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处,那么不同的搜寻方案有
A.80 种 B.70 种 C.40 种 D.10种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com