
分析 (1)利用函数y=Asin(ωx+φ)的周期为$\frac{2π}{ω}$,得出结论.
(2)利用正弦函数的定义域和值域,求得f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域,并求f(x)取得最大值时x的值.
解答 解(1)函数f(x))=$2sin(2x+\frac{π}{6})$ 的最小正周期T=$\frac{2π}{2}$=π.
(2)由-$\frac{π}{6}$≤x≤$\frac{π}{2}$,知-$\frac{π}{3}$≤2x≤π,故$-\frac{π}{6}≤2x+\frac{π}{6}≤\frac{7π}{6}$,∴$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,故$-1≤2sin(2x+\frac{π}{6})≤2$,
∴f(x)在区间[-$\frac{π}{6}$,$\frac{π}{2}$]上的值域[-1,2].
当 2x+$\frac{π}{6}$=$\frac{π}{2}$时,即 x=$\frac{π}{6}$时,f(x)取得最大值为2.
点评 本题主要考查函数y=Asin(ωx+φ)的周期性,正弦函数的定义域和值域,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
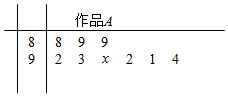 某校开展“向感动中国2015年度人物学习”主题墙报评比,9位评委为A班的墙报,给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
某校开展“向感动中国2015年度人物学习”主题墙报评比,9位评委为A班的墙报,给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
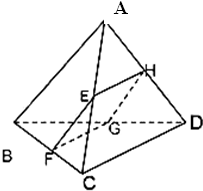 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
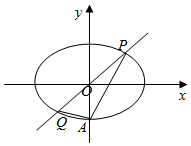 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com