
| 1 |
| 2 |
| ||
| 2 |
| 3a |
| 4 |
| ||
| 4 |
3
| ||
| 19 |


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
| A、14 | B、12 | C、9 | D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| QB |
| PB |
| QA |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 空气质量指数(AQI) | 国家环保标准 | 频数(天) | 频率 |
| [0,50] | 一级(优) | 4 | |
| (50,100] | 二级(良) | 20 | |
| (100,150] | 三级(轻度污染) | 8 | |
| (150,200] | 四级(中度污染) | 4 | |
| (200,300] | 五级(重度污染) | 3 | |
| (300,+∞] | 六级(严重污染) | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
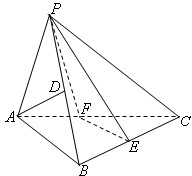 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.| AF |
| FC |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.05 | m | 0.15 | 0.35 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆E:
如图,已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 4 |
| 3 |
| OA |
| OB |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com