
| A. | -$\frac{119}{169}$ | B. | $\frac{119}{169}$ | C. | $\frac{120}{169}$ | D. | -$\frac{119}{169}$或$\frac{119}{169}$ |
分析 首先根据已知条件确定等腰三角形的角的关系式,进一步利用三角函数的诱导公式以及二倍角公式求出结果.
解答 解:设等腰△ABC的底角为A=B,顶角为C,
则sinA=$\frac{5}{13}$,
根据A+$\frac{1}{2}$C=$\frac{π}{2}$,
所以sinA=sin($\frac{π}{2}$-$\frac{1}{2}$C)=cos$\frac{1}{2}$C=$\frac{5}{13}$,
则:cos∠C=2cos2$\frac{C}{2}$-1=2×($\frac{5}{13}$)2-1=-$\frac{119}{169}$.
故选:A.
点评 本题考查的知识要点:等腰三角形的性质、二倍角公式、三角函数诱导公式的应用,三角函数值的求法.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<t<$\frac{1}{2}$ | B. | $\frac{1}{2}$<t<1 | C. | $\frac{\sqrt{2}}{2}$<t<$\sqrt{2}$ | D. | $\sqrt{2}$<t<$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
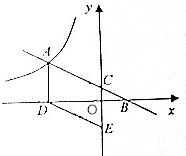 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|0<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com