
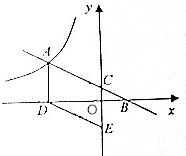
 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.分析 (1)设函数y=ax+b与y=$\frac{k}{x}$图象的交点A(m,$\frac{k}{m}$),判断四边形ADEC是平行四边形,利用面积公式列出方程求出k的值;
(2)根据题意设出点A、B、C的坐标,列出方程组求出对应的坐标,即可求出点E的坐标.
解答 解:(1)设函数y=ax+b与y=$\frac{k}{x}$图象的交点A(m,$\frac{k}{m}$),其中m<0;
则|AD|=$\frac{k}{m}$,|OD|=|m|=-m,
又DE∥AB,且AD∥CD,
∴四边形ADEC是平行四边形,其面积为
|CE|•|OD|=$\frac{k}{m}$•(-m)=6,
解得k=-6;
(2)∵k=-6,∴y=$\frac{-6}{x}$;
设函数y=ax+b与y=$\frac{-6}{x}$(x<0)图象的交点A(m,$\frac{-6}{m}$),其中m<0;
且与x轴、y轴分别交于点B(-$\frac{b}{a}$,0)、C(0,b),
则点D(m,0),且AD=CE;
∵AD=3OC,∴$\frac{-6}{m}$=3b①;
又tan∠DAC=2,∴-$\frac{b}{a}$-m=2•$\frac{-6}{m}$②;
又$\frac{-6}{m}$=am+b③,
由①②③组成方程组,解得m=-2$\sqrt{2}$,a=-$\frac{1}{2}$,b=$\frac{\sqrt{2}}{2}$;
∴OE=2OC=$\sqrt{2}$,
则点E(0,-$\sqrt{2}$).
点评 本题考查了一次函数与反比例函数的应用问题,也考查了方程思想与数形结合思想的应用问题,是综合性题目.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{119}{169}$ | B. | $\frac{119}{169}$ | C. | $\frac{120}{169}$ | D. | -$\frac{119}{169}$或$\frac{119}{169}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 若函数f(x)=cos(ωx+φ),ω>0,|φ|<$\frac{π}{2}$)的一个零点与之相邻的对称轴之间的距离为$\frac{π}{4}$,且x=$\frac{2π}{3}$时f(x)有最小值.
若函数f(x)=cos(ωx+φ),ω>0,|φ|<$\frac{π}{2}$)的一个零点与之相邻的对称轴之间的距离为$\frac{π}{4}$,且x=$\frac{2π}{3}$时f(x)有最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | ($\overrightarrow{b}$+$\overrightarrow{c}$)⊥($\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{a}$ | D. | $\overrightarrow{b}$•$\overrightarrow{c}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com