
| A. | $\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | ($\overrightarrow{b}$+$\overrightarrow{c}$)⊥($\overrightarrow{b}$-$\overrightarrow{c}$) | C. | $\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{a}$ | D. | $\overrightarrow{b}$•$\overrightarrow{c}$=0 |
分析 由题意可知|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,于是($\overrightarrow{b}$+$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=${\overrightarrow{b}}^{2}$-${\overrightarrow{c}}^{2}$=0.
解答 解:∵$\overrightarrow{b}$=$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$.∴$\overrightarrow{b}$为与$\overrightarrow{a}$同向的单位向量,
又∵$\overrightarrow{c}$=(cosθ,sinθ),∴|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1,
∴($\overrightarrow{b}$+$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=${\overrightarrow{b}}^{2}$-${\overrightarrow{c}}^{2}$=1-1=0,
∴($\overrightarrow{b}$+$\overrightarrow{c}$)⊥($\overrightarrow{b}$-$\overrightarrow{c}$).
故选:B.
点评 本题考查了平面向量的数量积运算,属于基础题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | 0<t<$\frac{1}{2}$ | B. | $\frac{1}{2}$<t<1 | C. | $\frac{\sqrt{2}}{2}$<t<$\sqrt{2}$ | D. | $\sqrt{2}$<t<$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
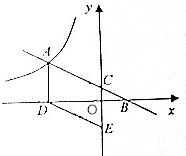 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (3,+∞) | C. | (-3,1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|0<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com