练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．在平面直角坐标系中，O为坐标原点，A，B，C三点满足$\overrightarrow{OC}$=$\frac{5}{3}$$\overrightarrow{OA}$-$\frac{2}{3}$$\overrightarrow{OB}$．
    （1）求证：A，B，C三点共线，并求$\frac{|\overrightarrow{AC|}}{|\overrightarrow{BC|}}$的值；
    （2）设A（1，sinx），B（1+cosx，2sinx），x∈R，求函数f（x）=$\overrightarrow{OA}$•$\overrightarrow{OB}$的最大值．

    分析 （1）利用向量的三角形法则、向量共线定理即可证明；
    （2）利用数量积运算性质、三角函数的单调性、二次函数的单调性即可得出．

    解答 （1）证明：∵A，B，C三点满足$\overrightarrow{OC}$=$\frac{5}{3}$$\overrightarrow{OA}$-$\frac{2}{3}$$\overrightarrow{OB}$，∴$\overrightarrow{OC}=\overrightarrow{OA}+\frac{2}{3}（\overrightarrow{OA}-\overrightarrow{OB}）$，
    化为$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{BA}$，
    ∴A，B，C三点共线，
    ∵$\overrightarrow{AC}=\frac{2}{3}\overrightarrow{BA}$，
    ∴$\overrightarrow{AC}$=$\frac{2}{3}$$（\overrightarrow{CA}-\overrightarrow{CB}）$，
    化为$\frac{5}{3}\overrightarrow{AC}=\frac{2}{3}\overrightarrow{BC}$，
    ∴$\frac{|\overrightarrow{AC|}}{|\overrightarrow{BC|}}$=$\frac{2}{5}$．
    （2）解：f（x）=$\overrightarrow{OA}$•$\overrightarrow{OB}$=1+cosx+2sin2x
    =1+cosx+2（1-cos2x）
    =-2$（cosx-\frac{1}{4}）^{2}$+$\frac{25}{8}$≤$\frac{25}{8}$，
    当cosx=$\frac{1}{4}$时，f（x）取得最大值$\frac{25}{8}$．

    点评 本题考查了向量的三角形法则、向量共线定理、数量积运算性质、三角函数的单调性、二次函数的单调性，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．f（x）=$\sqrt{πx}$+$\sqrt{2}$xcosx在点A（$\frac{π}{4}$，f（$\frac{π}{4}$））处的切线方程是y=（2-$\frac{π}{4}$）x+$\frac{4π+{π}^{2}}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．与圆x2+y2+4x-4y+7=0和x2+y2-4x-10y+13=0都相切的直线共有（　　）
    A．1条B．2条C．3条D．4条

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，在左支上过F1的弦AB的长为5，若2a=8，那么△ABF2的周长是（　　）
    A．16B．18C．21D．26

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．函数y=$\frac{1}{x-1}$的单调区间是（-∞，1）和（1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数y=sin（ωx+φ）（ω＞0，0＜φ＜π）满足f（-x）=f（x），其图象与直线y=1的某两个交点横坐标分别为x1，x2，且|x1-x2|的最小值为π，则（　　）
    A．$ω=\frac{1}{2}$，φ=$\frac{π}{4}$B．ω=2，φ=$\frac{π}{4}$C．$ω=\frac{1}{2}$，φ=$\frac{π}{2}$D．ω=2，φ=$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．若方程x2+y2-4x+6y=k2-14k表示一个圆，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

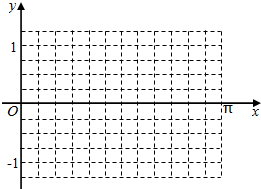    15．已知向量$\overrightarrow m=（asinx+cosx，1），\overrightarrow n=（cosx，-\frac{1}{2}）$，函数f（x）=$\overrightarrow m•\overrightarrow n$的图象的一条对称轴为直线x=$\frac{π}{6}$．
    （1）求a的值；
    （2）求函数f（x）的单调增区间；
    （3）作出函数f（x）在x∈[0，π]上的图象简图（列表，画图）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（$\sqrt{2}$，$\sqrt{3}$），左焦点F（-c，0）到直线bx+ay=0的距离为$\frac{\sqrt{3}b}{3}$．
    （1）求椭圆E的方程；
    （2）直线l过点F，与椭圆E交于不同两点A，B，椭圆E的右焦点为F′，求当△ABF′面积最大时直线l的方程．

    查看答案和解析>>

    同步练习册答案