
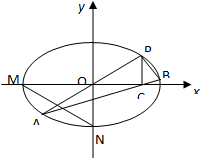
 已知直线x-y+1=0经过椭圆S:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>o)$的一个焦点和一个顶点.如图,M,N分别是椭圆S的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
已知直线x-y+1=0经过椭圆S:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>o)$的一个焦点和一个顶点.如图,M,N分别是椭圆S的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.分析 (I)在直线x-y+1=0中,分别令x=0,y=0,可得c=b=1,a2=b2+c2,即可得出椭圆的标准方程.利用中点坐标公式可得线段MN的中点坐标,可得k.
(II)将直线PA方程y=kx代入椭圆方程,解得:x=±$\frac{2}{\sqrt{1+2{k}^{2}}}$,令$\frac{2}{\sqrt{1+2{k}^{2}}}$=m,P(m,mk),A(-m,-mk),于是C(m,0),直线AB方程为y=$\frac{k}{2}$(x-m),代入椭圆方程得(k2+2)x2-2k2mx+k2m2-8=0,利用根与系数的关系可得:B.只要证明$\overrightarrow{AP}•\overrightarrow{PB}$=0,即可证明.
解答 解:(I)在直线x-y+1=0中,令x=0得y=1;令y=0得x=-1,由题意得c=b=1,
∴a2=2,
则椭圆方程为$\frac{{x}^{2}}{2}$+y2=1.
M(-$\sqrt{2}$,0),N(0,-1),
线段MN的中点坐标为$(-\frac{\sqrt{2}}{2},-\frac{1}{2})$,∴k=$\frac{\sqrt{2}}{2}$.
(II)将直线PA方程y=kx代入椭圆方程,
解得:x=±$\frac{2}{\sqrt{1+2{k}^{2}}}$,令$\frac{2}{\sqrt{1+2{k}^{2}}}$=m,
则P(m,mk),A(-m,-mk),于是C(m,0),
故直线AB方程为y=$\frac{0+mk}{m+m}$(x-m)=$\frac{k}{2}$(x-m),
代入椭圆方程得(k2+2)x2-2k2mx+k2m2-8=0,由xB+xA=$\frac{2{k}^{2}m}{{k}^{2}+2}$,
因此B$(\frac{3m{k}^{2}+2m}{{k}^{2}+2},\frac{m{k}^{3}}{{k}^{2}+2})$.
∴$\overrightarrow{AP}$=(2m,2mk),$\overrightarrow{PB}$=$(\frac{2m{k}^{2}}{{k}^{2}+2},\frac{-2mk}{{k}^{2}+2})$.
∴$\overrightarrow{AP}•\overrightarrow{PB}$=$\frac{4{m}^{2}{k}^{2}}{{k}^{2}+2}$-$\frac{4{m}^{2}{k}^{2}}{{k}^{2}+2}$=0,
∴$\overrightarrow{AP}⊥\overrightarrow{PB}$,因此PA⊥PB.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交、根与系数的关系、向量垂直与数量积的关系、向量中点坐标公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | β=90°+α | B. | α+β=180° | C. | α=90°+β | D. | α+β=90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+y+5=0 | B. | 2x-y-3=0 | C. | 3x-y-7=0 | D. | 3x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {〔1,1〕} | B. | {〔-1,1〕} | C. | {〔1,0〕} | D. | {〔0,1〕} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin|x| | B. | y=|sinx| | C. | $y=sin\frac{x}{2}$ | D. | $y=cos\frac{x}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 没有危害(人) | 有危害(人) | 合计 | |
| 喜欢吃零食 | 5 | 12 | |
| 不喜欢吃零食 | 40 | 28 | |
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com