
分析 (1)由已知向量的坐标结合向量共线的条件列式求得sinα,进一步得到cosα,再由二倍角公式求得sin2α的值;
(2)由已知求得cosα,得到tanα,求出$\overrightarrow{a},\overrightarrow{b}$的坐标,然后利用数量积证得答案.
解答 (1)解:∵$\overrightarrow{a}$=(5cosα,4),$\overrightarrow{b}$=(3,4tanα),且$\overrightarrow{a}∥\overrightarrow{b}$,
∴5cosα•4tanα-12=0,得20sinα=12,sin$α=\frac{3}{5}$,
∵α∈($\frac{π}{2}$,π),∴cosα=$-\frac{4}{5}$,
∴sin2α=2sinαcosα=$2×\frac{3}{5}×(-\frac{4}{5})=-\frac{24}{25}$;
(2)证明:$|\overrightarrow{a}|=\sqrt{25co{s}^{2}α+16}=5$,
得cosα=-$\frac{3}{5}$,则sinα=$\frac{4}{5}$,tanα=-$\frac{4}{3}$,
∴$\overrightarrow{a}$=(5cosα,4)=(-3,4),$\overrightarrow{b}$=(3,4tanα)=(3,-$\frac{16}{3}$),
则$\overrightarrow{a}+\overrightarrow{b}=(0,-\frac{4}{3})$,
∵$\overrightarrow{c}$=(2,0),
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=0×$2-\frac{4}{3}×0=0$.
则($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{c}$.
点评 本题考查平面向量的数量积运算,考查向量垂直与夹角的关系,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x3-1 | B. | f(x)=x+cosx | C. | f(x)=xsinx | D. | f(x)=lg(x+$\sqrt{{x}^{2}+1}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 爱好 | 40 | ||
| 不爱好 | 25 | ||
| 总计 | 45 | 100 |
| p(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
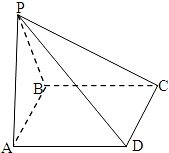 如图,在四棱锥P-ABCD中,面PAB⊥面ABCD,PA=PB=$\sqrt{3}$,且四边形ABCD为菱形,AD=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,面PAB⊥面ABCD,PA=PB=$\sqrt{3}$,且四边形ABCD为菱形,AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2010 | B. | 2010 | C. | 2011 | D. | -2011 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -80 | -24 | 0 | 4 | 0 | 0 | 16 | 60 | 144 | 280 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com