
已知函数f(x)=|sinx|的图象与直线y=kx(k>0)有且仅有三个交点,交点的横坐标的最大值为α,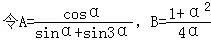 .则( )
.则( )
A.A>B B.A<B
C.A=B D.A与B的大小不确定
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:
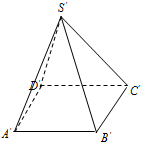 已知四棱锥S-ABCD的用斜二测画法画出的直观图如图所示,底面A′B′C′D′是一个平行四边形,其中∠B′A′D′=45°,A′B′=2cm,A′D′=1cm,直观图的高为3cm,则四棱锥S-ABCD的体积为( )
已知四棱锥S-ABCD的用斜二测画法画出的直观图如图所示,底面A′B′C′D′是一个平行四边形,其中∠B′A′D′=45°,A′B′=2cm,A′D′=1cm,直观图的高为3cm,则四棱锥S-ABCD的体积为( )| A、2cm3 | ||
| B、4cm3 | ||
C、
| ||
| D、6cm3 |
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
(2010•嘉兴一模)如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:选择题
图中∠BOD的度数是( )
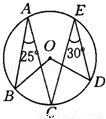
A.55° B.110° C.125° D.150°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
下列表述:①综合法是执因导果法;②综合法是顺推法;③分析法是执果索因法;
④分析法是间接证法;⑤反证法是逆推法.正确的语句有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
以下说法正确的是( )
A.在用综合法证明的过程中,每一个分步结论都是结论成立的必要条件
B.在用综合法证明的过程中,每一个分步结论都是条件成立的必要条件
C.在用分析法证明的过程中,每一个分步结论都是条件成立的充分条件
D.在用分析法证明的过程中,每一个分步结论都是结论成立的必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
证明命题:“f(x)=ex+ 在(0,+∞)上是增函数”,现给出的证法如下:
在(0,+∞)上是增函数”,现给出的证法如下:
因为f(x)=ex+ ,所以f′(x)=ex﹣
,所以f′(x)=ex﹣ ,
,
因为x>0,所以ex>1,0< <1,
<1,
所以ex﹣ >0,即f′(x)>0,
>0,即f′(x)>0,
所以f(x)在(0,+∞)上是增函数,使用的证明方法是( )
A.综合法 B.分析法 C.反证法 D.以上都不是
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•揭阳三模)对于正实数α,Mα为满足下述条件的函数f(x)构成的集合:?x1,x2∈R且x2>x1,有﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1).下列结论中正确的是( )
A.若f(x)∈Mα1,g(x)Mα2,则f(x)•g(x)∈Mα1•α2
B.若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则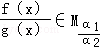
C.若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2
D.若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)﹣g(x)∈Mα1﹣α2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com