
分析 由条件利用两个向量的加减法及其几何意义,两个向量的数量积的定义和公式,一元二次不等式的解法,逐一判断各个选项是否正确,从而得出结论.
解答 解:由题意可得,$|{\overrightarrow a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos120°=-1,
∴|${\overrightarrow a$+$\overrightarrow b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{1-2+4}$=$\sqrt{3}$,故①正确.
若点D是边BC的中点,由$\overrightarrow{AB}$=$\overrightarrow{a}$+k$\overrightarrow{b}$,$\overrightarrow{AC}$=k$\overrightarrow{a}$+$\overrightarrow{b}$,可得$\overrightarrow{AD}$=$\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$=$\frac{k+1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),故②正确.
若∠A为直角,则$\overrightarrow{AB}•\overrightarrow{AC}$=($\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$+$\overrightarrow{b}$ )=k(${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$)+(k2+1)$\overrightarrow{a}•\overrightarrow{b}$=-k2+5k-1=0,求得k=$\frac{5±\sqrt{21}}{2}$,故③正确.
若∠A为钝角,则$\overrightarrow{AB}•\overrightarrow{AC}$=($\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$+$\overrightarrow{b}$ )=k(${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$)+(k2+1)$\overrightarrow{a}•\overrightarrow{b}$=-k2+5k-1<0,求得k<$\frac{5-\sqrt{21}}{2}$ 或k>$\frac{5+\sqrt{21}}{2}$,故④正确.
若∠A为锐角,则$\overrightarrow{AB}•\overrightarrow{AC}$=($\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$+$\overrightarrow{b}$ )=k(${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$)+(k2+1)$\overrightarrow{a}•\overrightarrow{b}$=-k2+5k-1>0,求得$\frac{5-\sqrt{21}}{2}$k<$\frac{5+\sqrt{21}}{2}$,故⑤正确.
故答案为:①②③④⑤.
点评 本题主要考查平面向量的数量积、夹角、运算法则,一元二次不等式的解法,体现了转化的数学思想,属于中档题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
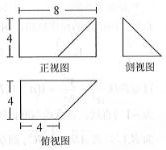 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.| 选定网站的日访问量n(单位:万次) | A公司的付费标准(单位:元/日) |
| n<25 | 500 |
| 25≤n≤35 | 700 |
| n>35 | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com