
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1,![]() ,
,![]() 为线段
为线段![]() ,
,![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面截该正方体的截面记为
的平面截该正方体的截面记为![]() ,则下列命题正确的是________.
,则下列命题正确的是________.
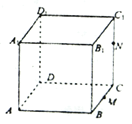
①当![]() 且
且![]() 时,
时,![]() 为等腰梯形;
为等腰梯形;
②当![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点时,几何体
的中点时,几何体![]() 的体积为
的体积为![]() ;
;
③当![]() 为
为![]() 中点且
中点且![]() 时,
时,![]() 与
与![]() 的交点为
的交点为![]() ,满足
,满足![]() ;
;
④当![]() 且
且![]() 时,
时, ![]() 的面积
的面积![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
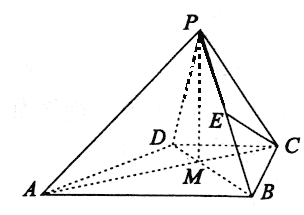
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 上位于第一象限的任意一点,过点
上位于第一象限的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.
(1)若当点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的方程;
的方程;
(2)对于(1)中求出的抛物线![]() ,若点
,若点![]() ,记点
,记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,求证:点
,求证:点![]() 的坐标为
的坐标为![]() ,并求点
,并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
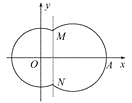
(1)求圆弧C2的方程.
(2)曲线C上是否存在点P,满足PA=![]() PO?若存在,指出有几个这样的点;若不存在,请说明理由.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,曲线C的参数方程是
轴的正半轴,建立平面直角坐标系,曲线C的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 被曲线C截得的弦长;
被曲线C截得的弦长;
(2)从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布列如下:
的分布列如下:
| 8 | 9 | 10 |
| 0.4 | 0.4 | 0.2 |
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(1)求该运动员两次命中的环数相同的概率;
(2)求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中有且只有两个偶数相邻,则这样的六位数的个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com