练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．下列函数既是奇函数又在（0，+∞）上为减函数的是（　　）
    A．y=-tanxB．y=$\frac{{e}^{-x}-{e}^{x}}{2}$C．y=ln$\frac{1-x}{1+x}$D．y=-x2+1

    分析 由函数的解析式考查所给函数的性质，排除错误选项即可求得最终结果．

    解答 解：利用排除法：
    函数y=-tanx在（0，+∞）不是单调函数，选项A错误；
    当x=1时，函数$y=ln\frac{1-x}{1+x}$ 没有意义，无法考查该函数在区间（0，+∞）上的单调性，选项C错误
    函数y=-x2+1 是偶函数，选项D错误，
    故选：B．

    点评 本题考查了函数的单调性，函数的奇偶性，函数的定义域等，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知关于实数x，y的二元一次不等式组$\left\{{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}}\right.$．
    （Ⅰ）在右下图坐标系内画出该不等式组所表示的平面区域，并求其面积；
    （Ⅱ）求$\frac{y}{x+1}$的取值范围；
    （Ⅲ）求x2+y2的最小值，并求此时x，y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知$\overrightarrow{AB}=（1，-1）$与垂直的单位向量的坐标是（　　）
    A．$（-\frac{{\sqrt{2}}}{2}，-\frac{{\sqrt{2}}}{2}）$B．$（\frac{{\sqrt{2}}}{2}，-\frac{{\sqrt{2}}}{2}）$C．$（-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}）$D．（-1，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若等差数列{an}中，a8-$\frac{1}{2}{a_{11}}$=6，则数列{an}的前9项和S9=108．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知直线l：2x+my-2-3m=0（m∈R）．
    （1）判断直线l与圆x2+y2-4x-6y+9=0的位置关系，并说明理由；
    （2）求实数m的取值范围，使得总能找到一个同事满足下列条件的圆与直线l相切：①面积为π；②其某条直径的两端点分别在两个坐标轴上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在△ABC中，已知其面积为S=a2-（b-c）2，则cosA=（　　）
    A．$\frac{3}{4}$B．$\frac{13}{15}$C．$\frac{15}{17}$D．$\frac{17}{19}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．直线（m+1）x+（m-1）y-2=0与圆（x-1）2+y2=1的位置关系是（　　）
    A．相交B．相切C．相离D．相交或相切

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在数列-1，0，$\frac{1}{9}$，$\frac{1}{8}$，…中，0.08是它的第几项（　　）
    A．10B．9C．11D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

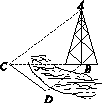    9．如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C与D，测得∠BCD=15°，∠BDC=135°，CD=30m，并在点C处测得塔顶A的仰角为30°，则塔高AB
    为（　　）
    A．10$\sqrt{2}$ mB．10$\sqrt{3}$ mC．15$\sqrt{6}$ mD．10$\sqrt{6}$ m

    查看答案和解析>>

    同步练习册答案