
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴交点为
轴交点为![]() ,与
,与![]() 的交点为
的交点为![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 相交于
相交于![]() 两点,且
两点,且![]() 四点在同一圆上,求
四点在同一圆上,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为![]() ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
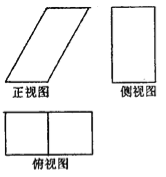
(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 与函数
与函数![]() 表示同一个函数;
表示同一个函数;
②奇函数的图像一定通过直角坐标系的原点;
③函数![]() 的图像可由
的图像可由![]() 的图像向右平移1个单位得到;
的图像向右平移1个单位得到;
④![]() 的最小值为1
的最小值为1
⑤对于函数f(x),若f(-1)![]() f(3)<0,则方程
f(3)<0,则方程![]() 在区间[-1,3]上有一实根;
在区间[-1,3]上有一实根;
其中正确命题的序号是 .(填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本25万元,此外每生产1件这样的产品,还需增加投入0.5万元,经市场调查知这种产品年需求量为500件,产品销售数量为t件时,销售所得的收入为![]() 万元.
万元.
(1)该公司这种产品的年生产量为x件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x);
(2)当该公司的年产量为多少件时,当年所获得的利润最大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com