
| A. | 6 | B. | 12 | C. | -6 | D. | -12 |
分析 建立平面直角坐标系,代入各点坐标计算
解答 解以AB所在直线为x轴,以A为坐标原点建立平面直角坐标系,
则A(0,0),B(4,0),C(5,$\sqrt{3}$),D(1,$\sqrt{3}$).E($\frac{9}{2}$,$\frac{\sqrt{3}}{2}$)
$\overrightarrow{AE}$=($\frac{9}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{BD}$=(-3,$\sqrt{3}$)
.$\overrightarrow{BD}$$•\overrightarrow{AE}$=$-\frac{27}{2}$$+\frac{3}{2}$=-12,
故选:D
点评 本题考查了平面向量的数量积运算,属于基础题


科目:高中数学 来源: 题型:解答题
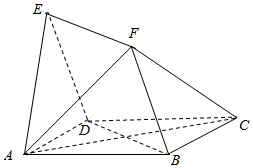 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,AB=2,且FA=FC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
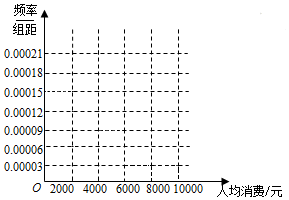 某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:| 人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
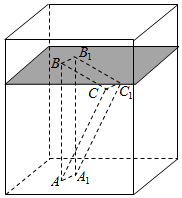 已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )
已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )| A. | 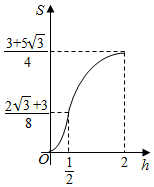 | B. | 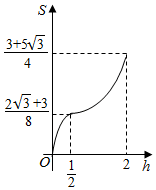 | ||
| C. | 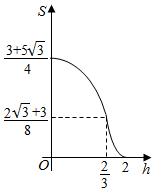 | D. | 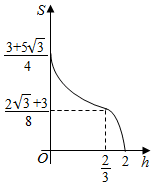 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q真 | B. | p∨q真 | C. | (¬p)∧q为假 | D. | (¬p)∧(¬q)为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com