
分析 将切化弦,利用两角和差的余弦公式化简,结合a=2c和余弦定理得出b,c的关系,利用三角形的面积列方程解出三角形的边长.
解答 解:∵c+bsinAtanB=4a+bcosA,∴ccosB+bsinAsinB=4acosB+bcosAcosB,
∴(c-4a)cosB=b(cosAcosB-sinAsinB)=bcos(A+B)=-bcosC.
∵sinA=2sinC,∴a=2c,
∴-7ccosB=-bcosC.
∴7c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=b×$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,即3a2+4c2-4b2=0,
∵a=2c,∴12c2+4c2=4b2,∴b=2c.
∴a=b=2c.
∴△ABC是等腰三角形,设AB边上的高为h,则h=$\sqrt{{a}^{2}-\frac{{c}^{2}}{4}}$=$\frac{\sqrt{15}}{2}c$.
∴S=$\frac{1}{2}ch$=$\frac{1}{2}×c×\frac{\sqrt{15}}{2}c$=$\sqrt{15}$.解得c=2.
∴a+c=3c=6.
故答案为6.
点评 本题考查了正余弦定理,三角函数的恒等变换,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,1,3} | B. | {-3,-1,1,3} | C. | {-1,1,3,5} | D. | {-3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
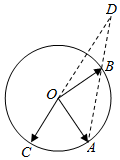 已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )
已知A,B,C为圆O上三点,CO的延长线与线段AB的延长线交于圆O外一点D,且|OD|=2|OC|,若$\overrightarrow{OC}$=p$\overrightarrow{OA}$+q$\overrightarrow{OB}$,则p+q的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com