已知函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R),且函数f(x)的图象关于原点
对称,其图象在x=3处的切线方程为8x-y-18=0
(1)求f(x)的解析式;
(2)是否存在区间[m,n],使得函数g(x)的定义域和值域均为[m,n],且其解析式为f(x)的解析式?若存在,求出这样一个区间[m,n];若不存在,则说明理由.
解:(1)∵f(x)的图象关于原点对称,
∴f(-x)+f(x)=0恒成立,
即2bx
2+2d=0,∴b=d=0
又f(x)的图象在x=3处的切线方程为8x-y-18=0,
即y-6=8(x-3),
∴f'(3)=8,且f(3)=6.而f(x)=ax
3+cx,
∴f'(x)=3ax
2+c
∴

.
故所求的解析式为
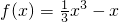
.
(2)解

又f'(x)=x
2-1,由f'(x)=0得x=±1,
且当

时,f'(x)>0;
当x∈(-1,1)时f'(x)<0.
∴

递增;在[-1,1]上递减
∴

上的极大值和极小值分别为

.
而
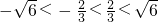
.
故存在这样的区间[m,n],其中一个区间为
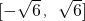
.
分析:(1)根据题意,f(-x)+f(x)=0恒成立,利用比较系数法可得b=d=0,然后根据导数的几何意义,得出f'(3)=8且f(3)=6,联解方程组可得a、c的值,最终可得f(x)的解析式;
(2)用直线y=x与函数y=f(x)联解,得出交点横坐标为

,根据题意得出[m,n]可能的区间为

.然后利用导数来研究函数f(x)的单调性,得出其单调区间后,分别讨论它在各区间上的值域,对照题意可得符合条件的区间为
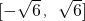
.
点评:本题考查了函数在某点取得极值的条件、利用导数求闭区间上函数的最值和导数的几何意义等知识点,属于中档题.

 .
.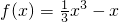 .
.
 时,f'(x)>0;
时,f'(x)>0; 递增;在[-1,1]上递减
递增;在[-1,1]上递减 上的极大值和极小值分别为
上的极大值和极小值分别为 .
.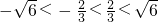 .
.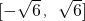 .
. ,根据题意得出[m,n]可能的区间为
,根据题意得出[m,n]可能的区间为 .然后利用导数来研究函数f(x)的单调性,得出其单调区间后,分别讨论它在各区间上的值域,对照题意可得符合条件的区间为
.然后利用导数来研究函数f(x)的单调性,得出其单调区间后,分别讨论它在各区间上的值域,对照题意可得符合条件的区间为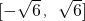 .
.
