解:(1)由f(x)=ln x+
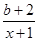
,得f′(x)=
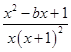
.
①证明:因为x>1时,h(x)=
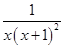
>0,所以函数f(x)具有性质P(b).
②当b≤2时,由x>1得x
2-bx+1≥x
2-2x+1=(x-1)
2>0,
所以f′(x)>0.从而函数f(x)在区间(1,+∞)上单调递增.
当b>2时,令x
2-bx+1=0得
x
1=
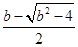
,x
2=
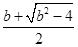
.
因为x
1=
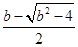
=
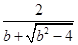
<
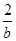
<1,
x
2=
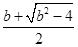
>1,
所以当x∈(1,x
2)时,f′(x)<0;当x∈(x
2,+∞)时,f′(x)>0;当x=x
2时,f′(x)=0.从而函数f(x)在区间(1,x
2)上单调递减,在区间(x
2,+∞)上单调递增.
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,
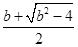
),单调增区间为(
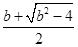
,+∞).
(2)由题设知,g(x)的导函数
g′(x)=h(x)(x
2-2x+1),
其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以当x>1时,g′(x)=h(x)(x-1)
2>0,
从而g(x)在区间(1,+∞)上单调递增.
①当m∈(0,1)时,
有α=mx
1+(1-m)x
2>mx
1+(1-m)x
1=x
1,
α<mx
2+(1-m)x
2=x
2,即α∈(x
1,x
2),
同理可得β∈(x
1,x
2).
所以由g(x)的单调性知g(α),g(β)∈(g(x
1),g(x
2)),从而有|g(α)-g(β)|<|g(x
1)-g(x
2)|,符合题意.
②当m≤0时,α=mx
1+(1-m)x
2≥mx
2+(1-m)x
2=x
2,β=(1-m)x
1+mx
2≤(1-m)x
1+mx
1=x
1,于是由α>1,β>1及g(x)的单调性知g(β)≤g(x
1)<g(x
2)≤g(α),
所以|g(α)-g(β)|≥|g(x
1)-g(x
2)|,与题意不符.
③当m≥1时,同理可得α≤x
1,β≥x
2,
进而得|g(α)-g(β)|≥|g(x
1)-g(x
2)|,与题意不符.
综上所述,所求的m的取值范围为(0,1).

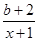 (x>1),其中b为实数.
(x>1),其中b为实数.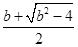 ),单调增区间为(
),单调增区间为(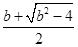 ,+∞).
,+∞).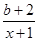 ,得f′(x)=
,得f′(x)=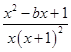 .
.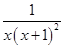 >0,所以函数f(x)具有性质P(b).
>0,所以函数f(x)具有性质P(b).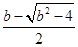 ,x2=
,x2=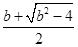 .
.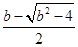 =
=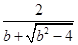 <
<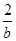 <1,
<1,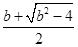 >1,
>1,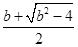 ),单调增区间为(
),单调增区间为(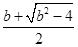 ,+∞).
,+∞).

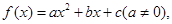 曲线y=f(x)通过点(0,2a+3),且在点
曲线y=f(x)通过点(0,2a+3),且在点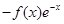 的单调区间.
的单调区间.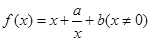 ,其中
,其中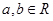 .
.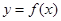 在点
在点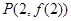 处的切线方程为
处的切线方程为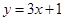 ,求函数
,求函数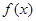 的解析式;
的解析式;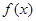 的单调性;
的单调性;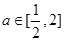 ,不等式
,不等式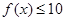 在
在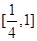 上恒成立,求
上恒成立,求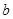 的取值范围.
的取值范围.