
已知椭圆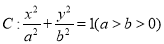 ,离心率为
,离心率为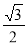 ,两焦点分别为
,两焦点分别为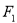 、
、 ,过
,过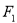 的直线交椭圆
的直线交椭圆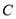 于
于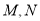 两点,且△
两点,且△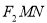 的周长为
的周长为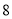 .
.
(1)求椭圆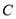 的方程;
的方程;
(2)过点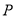
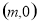 作圆
作圆 的切线
的切线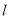 交椭圆
交椭圆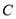 于
于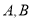 两点,求弦长
两点,求弦长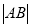 的最大值.
的最大值.
(1)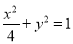 ;(2)2.
;(2)2.
【解析】
试题分析:(1)确定椭圆标准方程需要两个独立条件,由离心率为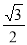 得
得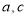 的关系,由椭圆定义得△
的关系,由椭圆定义得△ 的周长为
的周长为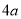 ,从而可求得
,从而可求得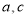 ,进而可确定椭圆方程;(2)解析几何中的最值问题,通常是选定变量,将目标函数用一个变量表示,进而转化为求函数的最值问题.本题中当斜率不存在时,则切线为
,进而可确定椭圆方程;(2)解析几何中的最值问题,通常是选定变量,将目标函数用一个变量表示,进而转化为求函数的最值问题.本题中当斜率不存在时,则切线为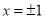 ,此时直接计算弦长
,此时直接计算弦长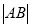 ;当切线斜率存在时,可设直线方程
;当切线斜率存在时,可设直线方程 利用直线和圆相切的条件,得变量
利用直线和圆相切的条件,得变量 的关系,利用斜长公式结合韦达定理,将
的关系,利用斜长公式结合韦达定理,将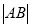 用变量
用变量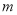 表示,进而求函数
表示,进而求函数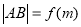 的最大值即可.
的最大值即可.
试题解析:(1)由题得: ,
,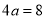 ,所以
,所以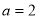 ,
, 。 3分
。 3分
又 ,所以
,所以 即椭圆
即椭圆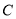 的方程为
的方程为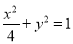 . 4分
. 4分
(2)由题意知,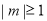 .
.
当 时,切线l的方程
时,切线l的方程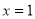 ,点A、B的坐标分别为
,点A、B的坐标分别为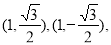
此时 ; 当m=-1时,同理可得
; 当m=-1时,同理可得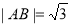 5分
5分
当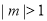 时,设切线
时,设切线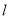 的方程为
的方程为
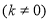
由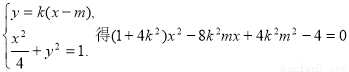
设A、B两点的坐标分别为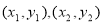 ,
,
则 

又由l与圆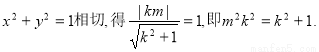 得
得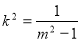
所以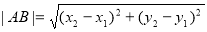
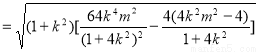
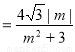 9分
9分
因为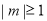 所以
所以
且当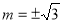 时,|AB|=2,
时,|AB|=2,
由于当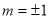 时,
时,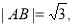 所以|AB|的最大值为2. 12分
所以|AB|的最大值为2. 12分
考点:1、椭圆的标准方程和简单几何性质;2、函数的最值.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:2015届广东惠州市高三第二次调研考试文科数学试卷(解析版) 题型:选择题
复数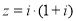 (
(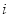 为虚数单位)在复平面上对应的点位于 ( )
为虚数单位)在复平面上对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考理科数学试卷(解析版) 题型:选择题
点 均在同一球面上,且
均在同一球面上,且 、
、 、
、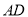 两两垂直,且
两两垂直,且
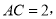
 ,则该球的表面积为( )
,则该球的表面积为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考文科数学试卷(解析版) 题型:填空题
已知函数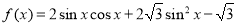 ,将
,将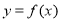 的图像向左平移
的图像向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数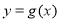 的图象,若函数
的图象,若函数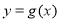 在
在 上至少含有
上至少含有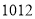 个零点,则
个零点,则 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考文科数学试卷(解析版) 题型:选择题
在平面直角坐标系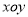 中,抛物线
中,抛物线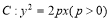 的焦点为
的焦点为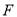 ,
,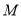 为抛物线
为抛物线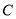 上一点,若△
上一点,若△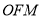 的外接圆与抛物线
的外接圆与抛物线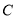 的准线相切,且外接圆的面积为
的准线相切,且外接圆的面积为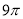 ,则
,则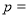 ( )
( )
A.2 B.4 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高三上学期期中联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知p:函数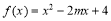 在
在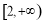 上单调递增;q:关于
上单调递增;q:关于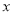 的不等式
的不等式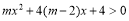 的解集为R.若
的解集为R.若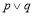 为真命题,
为真命题,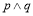 为假命题,求
为假命题,求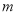 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com