
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 依据题意先求出椭圆的右焦点坐标、右准线方程,以及圆的半径,利用圆被椭圆的右准线分成弧长为2:1的两段弧,构造直角三角形,利用直角三角形中的边角关系求出离心率.
解答 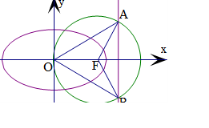 解:椭圆的右焦点F(c,0),右准线为x=$\frac{{a}^{2}}{c}$,圆的半径为c,
解:椭圆的右焦点F(c,0),右准线为x=$\frac{{a}^{2}}{c}$,圆的半径为c,
圆与右准线的两个交点A,D两点的横坐标为$\frac{{a}^{2}}{c}$,
∵圆被椭圆的右准线分成弧长为2:1的两段弧,∴∠AFD=120°,
∴△OAD是正三角形,由FA=FD,及∠AFD=120°,
构造直角三角形,利用边角关系得:
cos60°=$\frac{1}{2}$=$\frac{\frac{{a}^{2}}{c}-c}{c}$,
∴$\frac{{c}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,
故选:B.
点评 本题考查椭圆的标准方程和简单性质,利用直角三角形中的边角关系求出离心率.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
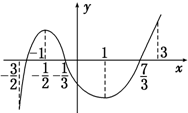 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{4}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{-\sqrt{2},1}]$ | C. | $[{-1,\sqrt{2}}]$ | D. | $[{-\sqrt{2},\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$(e x-e -x) | B. | $\frac{1}{2}$(e x+e -x) | C. | e x-e -x | D. | e x+e -x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com