
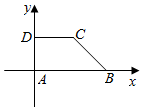
 如图直角梯形ABCD中,|AB|=2,|DC|=1,|AD|=1,点P为梯形ABCD内部(包括边界)内任一点,则$\overrightarrow{AP}$•$\overrightarrow{BD}$的取值范围为[-4,1].
如图直角梯形ABCD中,|AB|=2,|DC|=1,|AD|=1,点P为梯形ABCD内部(包括边界)内任一点,则$\overrightarrow{AP}$•$\overrightarrow{BD}$的取值范围为[-4,1]. 分析 可得出A,B,C,D四点坐标,并设P(x,y),从而得出$\overrightarrow{AP},\overrightarrow{BD}$的坐标,进而求出$\overrightarrow{AP}•\overrightarrow{BD}=-2x+y$,可设-2x+y=z,得到y=2x+z,z表示直线y=2x+z在y轴上的解决,x,y的变化范围为矩形ABCD及其内部,这样根据线性规划的知识即可求出z的最大、最小值,从而求出z的范围,即得出$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围.
解答 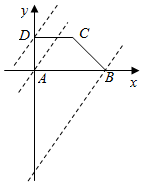 解:由条件,A(0,0),B(2,0),C(1,1),D(0,1),设P(x,y),则:
解:由条件,A(0,0),B(2,0),C(1,1),D(0,1),设P(x,y),则:
$\overrightarrow{AP}=(x,y),\overrightarrow{BD}=(-2,1)$;
∴$\overrightarrow{AP}•\overrightarrow{BD}=-2x+y$;
设-2x+y=z,则y=2x+z,z表示直线y=2x+z在y轴上的截距,如图:
当直线过D(0,1)时截距最大为1,经过B(2,0)时截距最小为-4;
∴-4≤z≤1;
∴$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围为[-4,1].
故答案为:[-4,1].
点评 考查利用向量坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标可求向量的坐标,向量数量积的坐标运算,线性规划的概念,以及利用线性规划求变量范围的方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {-2,4} | C. | {-2,2,4} | D. | {-4,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个长度单位 | B. | 向右平移$\frac{π}{4}$个长度单位 | ||
| C. | 向左平移$\frac{π}{2}$个长度单位 | D. | 向右平移$\frac{π}{2}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3 | B. | 0.5 | C. | 0.1 | D. | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,3) | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 134石 | B. | 169石 | C. | 192石 | D. | 338石 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com