
分析 由同角三角函数关系得sin(α+$\frac{π}{6}$)=$\frac{3}{5}$,由二倍角公式得tan[2(α+$\frac{π}{6}$)]=$\frac{24}{7}$,由两角差的正切公式得结果.
解答 解:∵cos(α+$\frac{π}{6}$)=$\frac{4}{5}$,α∈(0,$\frac{π}{2}$),
∵cos2(α+$\frac{π}{6}$)+sin2(α+$\frac{π}{6}$)=1,α+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{π}{2}$)
∴sin(α+$\frac{π}{6}$)=$\frac{3}{5}$,
∴tan(α+$\frac{π}{6}$)=$\frac{3}{4}$,
∴tan[2(α+$\frac{π}{6}$)]=$\frac{2tan(α+\frac{π}{6})}{1-ta{n}^{2}(α+\frac{π}{6})}$=$\frac{24}{7}$,
∴tan(2α+$\frac{π}{12}$)=tan(2α+$\frac{π}{3}$-$\frac{π}{4}$)=tan[2(α+$\frac{π}{6}$)-$\frac{π}{4}$]=$\frac{17}{31}$.
点评 本题考查同角三角函数关系、二倍角公式、两角差的正切公式.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AP}$=-$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AP}$=-$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
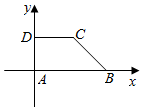 如图直角梯形ABCD中,|AB|=2,|DC|=1,|AD|=1,点P为梯形ABCD内部(包括边界)内任一点,则$\overrightarrow{AP}$•$\overrightarrow{BD}$的取值范围为[-4,1].
如图直角梯形ABCD中,|AB|=2,|DC|=1,|AD|=1,点P为梯形ABCD内部(包括边界)内任一点,则$\overrightarrow{AP}$•$\overrightarrow{BD}$的取值范围为[-4,1].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com