
分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:由f(x)=sinx-cosx+x+1,0<x<2π,
得f'(x)=cosx+sinx+1,
于是$f'(x)=1+\sqrt{2}sin({x+\frac{π}{4}})$.
令f'(x)=0,从而$sin({x+\frac{π}{4}})=-\frac{{\sqrt{3}}}{2}$,
得x=π或$x=\frac{3π}{2}$.
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (0,π) | π | $({0,\frac{3}{2}π})$ | $\frac{3}{2}π$ | $({\frac{3}{2}π,2π})$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | π+2 | 单调递减 | $\frac{3}{2}π$ | 单调递增 |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及三角函数问题,是一道中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
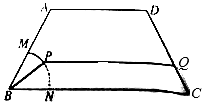 如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.
如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com