
分析 P的轨迹为线段C1C2的中垂线:2x+6y-10=0,由a2+b2-6a-4b+13=(a-3)2+(b-2)2,得到a2+b2-6a-4b+13的最小值是点(3,2)到直线2x+6y-10=0的距离的平方,由此能求出结果.
解答 解:∵圆${C_1}:{x^2}+{y^2}=4$与圆${C_2}:{(x-1)^2}+{(y-3)^2}=4$,
∴C1(0,0),C2(1,3),
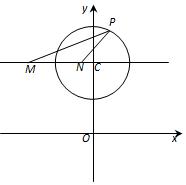
∵过动点P(a,b)分别作圆C1、圆C2的切线PM,PN,( M,N分别为切点),|PM|=|PN|,
∴P的轨迹为线段C1C2的中垂线,
线段C1C2的中点坐标为($\frac{1}{2}$,$\frac{3}{2}$),线段C1C2的斜率k′=$\frac{3}{1}$=3,
∴P的轨迹方程为$y-\frac{3}{2}=-\frac{1}{3}(x-\frac{1}{2})$,即2x+6y-10=0,
∵a2+b2-6a-4b+13=(a-3)2+(b-2)2,
∴a2+b2-6a-4b+13的最小值是点(3,2)到直线2x+6y-10=0的距离的平方,
∴a2+b2-6a-4b+13的最小值为:
d2=($\frac{|2×3+6×2-10|}{\sqrt{4+36}}$)2=$\frac{8}{5}$.
故答案为:$\frac{8}{5}$.
点评 本题考查代数式的最小值的求法,涉及到直线方程、圆、圆的切线方程、线段的中垂线方程、两点间距离公式、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0
已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| A. | 0.25% | B. | 2.5% | C. | 97.5% | D. | 99.75% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com