
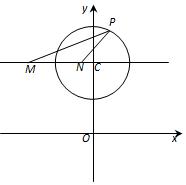
 已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0
已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0分析 (Ⅰ)利用直线系方程的特征,直接求解直线l过定点A的坐标.
(Ⅱ)当AC⊥l时,所截得弦长最短,由题知C(0,4),r=2,求出AC的斜率,利用点到直线的距离,转化求解即可.
(Ⅲ)法一:由题知,直线MC的方程为y=4,假设存在定点N(t,4)满足题意,
则设P(x,y),$\frac{|PM|}{|PN|}=λ$,得|PM|2=λ2|PN|2(λ>0),且(y-4)2=4-x2,求出λ,然后求解比值.
法二:设直线MC上的点N(t,4)取直线MC与圆C的交点P1(-2,4),则$\frac{|PM|}{|PN|}=\frac{1}{|t+2|}$,取直线MC与圆C的交点P2(2,4),则$\frac{|PM|}{|PN|}=\frac{5}{|t-2|}$,通过令$\frac{1}{|t+2|}=\frac{5}{|t-2|}$,存在这样的定点N满足题意,则必为$N(-\frac{4}{3},4)$,然后证明即可.
解答 解:(Ⅰ)依题意得,m(3x-y)+(x+y-4)=0,
令3x-y=0且x+y-4=0,得x=1,y=3∴直线l过定点A(1,3),
(Ⅱ)当AC⊥l时,所截得弦长最短,由题知C(0,4),r=2,
∴${k_{AC}}=\frac{4-3}{0-1}=-1$,得${k_l}=\frac{-1}{{{k_{AC}}}}=\frac{-1}{-1}=1$,∴由$\frac{3m+1}{m-1}=1$得m=-1,
∴圆心到直线的距离为$d=|AC|=\sqrt{2}$,
∴最短弦长为$l=2\sqrt{{r^2}-{d^2}}=2\sqrt{4-2}=2\sqrt{2}$.
(Ⅲ)法一:由题知,直线MC的方程为y=4,假设存在定点N(t,4)满足题意,
则设P(x,y),$\frac{|PM|}{|PN|}=λ$,得|PM|2=λ2|PN|2(λ>0),且(y-4)2=4-x2
∴(x+3)2+(y-4)2=λ2(x-t)2+λ2(y-4)2
∴(x+3)2+4-x2=λ2(x-t)2+λ2(4-x2)
整理得,(6+2tλ2)x-(λ2t2+4λ2-13)=0
∵上式对任意x∈[-2,2]恒成立,
∴6+2tλ2=0且λ2t2+4λ2-13=0
解得$t=-\frac{4}{3},λ=\frac{3}{2}$或t=-3,λ=1(舍去,与M重合)
综上可知,在直线MC上存在定点$N(-\frac{4}{3},4)$,使得$\frac{|PM|}{|PN|}$为常数$\frac{3}{2}$
法二:设直线MC上的点N(t,4)
取直线MC与圆C的交点P1(-2,4),则$\frac{|PM|}{|PN|}=\frac{1}{|t+2|}$
取直线MC与圆C的交点P2(2,4),则$\frac{|PM|}{|PN|}=\frac{5}{|t-2|}$
令$\frac{1}{|t+2|}=\frac{5}{|t-2|}$,解得$t=-\frac{4}{3}$或t=-3(舍去,与M重合),此时$\frac{|PM|}{|PN|}=\frac{3}{2}$
若存在这样的定点N满足题意,则必为$N(-\frac{4}{3},4)$,
下证:点$N(-\frac{4}{3},4)$满足题意,
设圆上任意一点P(x,y),则(y-4)2=4-x2
∴$\frac{{|PM{|^2}}}{{|PN{|^2}}}=\frac{{{{(x+3)}^2}+{{(y-4)}^2}}}{{{{(x+\frac{4}{3})}^2}+{{(y-4)}^2}}}=\frac{{{x^2}+6x+9+4-{x^2}}}{{{x^2}+\frac{8}{3}x+\frac{16}{9}+4-{x^2}}}$=$\frac{6x+13}{{\frac{8}{3}x+\frac{52}{9}}}=\frac{6x+13}{{\frac{4}{9}(6x+13)}}$=$\frac{9}{4}$,
∴$\frac{|PM|}{|PN|}=\frac{3}{2}$
综上可知,在直线MC上存在定点$N(-\frac{4}{3},4)$,使得$\frac{|PM|}{|PN|}$为常数$\frac{3}{2}$.
点评 本题考查直线与圆的方程的综合应用,考查转化思想以及计算能力.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sin\sqrt{2}<cos\sqrt{2}<tan\sqrt{2}$ | B. | $cos\sqrt{2}<sin\sqrt{2}<tan\sqrt{2}$ | C. | $cos\sqrt{2}<tan\sqrt{2}<sin\sqrt{2}$ | D. | $sin\sqrt{2}<tan\sqrt{2}<cos\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com