

分析 由题意,考察相邻两项的关系可得出f(n)-f(n-1)=4×(n-1),由累加法可求得f(n)=2n(n-1)+1,由此可求出答案.
解答 解:由题意,因为f(1)=1,f(2)=5,f(3)=13,f(4)=25
所以f(2)-f(1)=4,f(3)-f(2)=8=4×2,f(4)-f(3)=12=4×3,
由此可归纳出f(n)-f(n-1)=4×(n-1),
把上述等式依次相加可得f(n)-f(1)=4×[1+2+3+…+(n-1)]=2n(n-1)
∴f(n)=2n(n-1)+1
∴f(6)=61,
故答案为:61
点评 本题考查归纳推理,解题的关键是研究相邻两项的关系得出递推公式,再由累加法得出项的表达式,本题考察了分析归纳的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
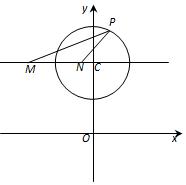 已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0
已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | n |
| A. | 1% | B. | 2.5% | C. | 5% | D. | 10% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com