练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知△ABC中，角A，B，C对应的分别是a，b，c，若a=4，b=6，C=60°．
    （1）求$\overrightarrow{BC}•\overrightarrow{CA}$；
    （2）求$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影．

    分析 （1）利用平面向量的数量积公式求得；
    （2）利用平面向量的数量积公式的几何意义求得即可．

    解答 解：（1）因为-a=4，b=6，C=60°．所以$\overrightarrow{BC}•\overrightarrow{CA}$=abcos（180°-60°）=4×6×（$-\frac{1}{2}$）=-12；
    （2）$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影为$|\overrightarrow{CA}|cos（180°-C）$=6×$（-\frac{1}{2}）$=-3．

    点评 本题考查了平面向量数量积的公式以及几何意义的运用；熟练掌握数量积公式的意义是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知集合A={f（x）|f（x）+f（x+2）=f（x+1）}，$g（x）=sin（\frac{πx}{3}）$．
    （1）求证：g（x）∈A；
    （2）g（x）是周期函数，据此猜想A中的元素一定是周期函数，判断该猜想是否正确，并证明你的结论；
    （3）g（x）是奇函数，据此猜想A中的元素一定是奇函数，判断该猜想是否正确，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=\frac{x^2}{{1+{x^2}}}$．
    （1）分别求$f（2）+f（{\frac{1}{2}}），f（3）+f（{\frac{1}{3}}），f（4）+f（{\frac{1}{4}}）$的值，并归纳猜想一般性结论（不要求证明）；
    （2）求值：$2f（2）+2f（3）+…+2f（{2017}）+f（{\frac{1}{2}}）+f（{\frac{1}{3}}）+…f（{\frac{1}{2017}}）+\frac{1}{2^2}f（2）+\frac{1}{3^2}f（3）+…+\frac{1}{{{{2017}^2}}}•f（{2017}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．图（1）、（2）、（3）、（4）分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”，按同样的方式构造图形，设第n个图形包含f（n）个“福娃迎迎”．则f（6）=61．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

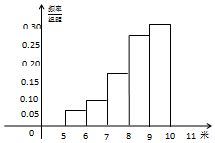    6．某市为了解今年高中毕业生的身体素质状况，从本市某校高中毕业班中抽取一个班进行实心球测试，成绩在8米及以上的为合格．把所得数据整理后，分成六组得到频率分布直方图的一部分（如图）．已知前五个小组的频率分别为0.06.0.10，0.14，0.28，0.30．第六小组的频数是6．
    （1）求这次测试合格的人数；
    （2）用分层抽样方法在第5、6组的学生中抽取容量为7的一个样本，将该样本看作一个总体，从中抽取2人，求恰有一人在第六组的概率．
    （3）经过多次测试发现，甲的成绩在8～10米之间，乙的成绩在9～10米之间现两人各投一次，求甲投得比乙远的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．$cos\sqrt{2}，sin\sqrt{2}，tan\sqrt{2}$的大小关系是（　　）
    A．$sin\sqrt{2}＜cos\sqrt{2}＜tan\sqrt{2}$B．$cos\sqrt{2}＜sin\sqrt{2}＜tan\sqrt{2}$C．$cos\sqrt{2}＜tan\sqrt{2}＜sin\sqrt{2}$D．$sin\sqrt{2}＜tan\sqrt{2}＜cos\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=cos（3x+φ）的图象关于原点成中心对称，则φ等于（　　）
    A．-$\frac{π}{2}$B．2kπ-$\frac{π}{2}$（k∈Z）C．kπ（k∈Z）D．kπ+$\frac{π}{2}$（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设点$F（{0，\frac{1}{4}}）$，动圆A经过点F且和直线$y=-\frac{1}{4}$相切，记动圆的圆心A的轨迹为曲线C．
    （1）求曲线C的方程；
    （2）设曲线C上一点P的横坐标为t（t＞0），过P的直线交C于一点Q，交x轴于点M，过点Q作PQ的垂线交C于另一点N，若MN是C的切线，求t的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

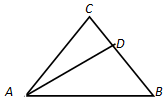
    1．如图所示，在△ABC中，BD=2CD，若$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，则$\overrightarrow{AD}$=（　　）
    A．$\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$B．$\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$C．$\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$D．$\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$

    查看答案和解析>>

    同步练习册答案