
分析 (1)代值计算即可,并猜想一般的结论,
(2)由(1)$f(x)+f({\frac{1}{x}})=1$,即可得出结论.
解答 解:(1)∵$f(x)=\frac{x^2}{{1+{x^2}}}$,
∴$f(2)+f({\frac{1}{2}})=\frac{2^2}{{1+{2^2}}}+\frac{{{{({\frac{1}{2}})}^2}}}{{1+{{({\frac{1}{2}})}^2}}}=\frac{2^2}{{1+{2^2}}}+\frac{1}{{1+{2^2}}}=1$,
同理可得$f(3)+f({\frac{1}{3}})=1,f(4)+f({\frac{1}{4}})=1$,
猜想$f(x)+f({\frac{1}{x}})=1$.
(2)∵$f(x)+\frac{1}{x^2}f(x)=\frac{x^2}{{1+{x^2}}}({1+\frac{1}{x^2}})=1$,
又由(1)得,$f(x)+f({\frac{1}{x}})=1$,
则$2f(2)+2f(3)+…2f({2017})+f({\frac{1}{2}})+f({\frac{1}{3}})+…f({\frac{1}{2017}})+\frac{1}{2^2}f(2)+\frac{1}{3^2}f(3)+…\frac{1}{{{{2017}^2}}}f({2017})$
=$[{f(2)+f({\frac{1}{2}})+f(2)+\frac{1}{2^2}f({\frac{1}{2}})}]+[{f(3)+f({\frac{1}{3}})+f(3)+\frac{1}{3^2}f({\frac{1}{3}})}]+$$…[{f({2017})+f({\frac{1}{2017}})+f({2017})+\frac{1}{{{{2017}^2}}}f({\frac{1}{2017}})}]=2×2016=4032$.
点评 本题考查归纳推理,考查学生的计算能力,正确归纳是关键,属于中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
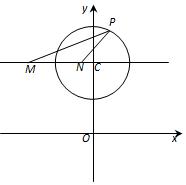 已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0
已知圆C:x2+(y-4)2=4,直线l:(3m+1)x+(1-m)y-4=0查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 10 | 40 | 50 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 30 | 70 | n |
| A. | 1% | B. | 2.5% | C. | 5% | D. | 10% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
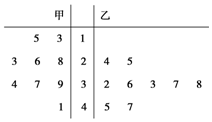 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$,$\overline{x_乙}$;准差分别是s甲,s乙,则有( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$,$\overline{x_乙}$;准差分别是s甲,s乙,则有( )| A. | $\overline{x_甲}$<$\overline{x_乙}$,s甲<s乙 | B. | $\overline{x_甲}$<$\overline{x_乙}$,s甲>s乙 | ||
| C. | $\overline{x_甲}$>$\overline{x_乙}$,s甲<s乙 | D. | $\overline{x_甲}$>$\overline{x_乙}$,s甲>s乙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com