
分析 (1)根据抛物线的定义,求出抛物线的解析式即可;
(2)求出直线PQ的方程,求出M的坐标,联立方程组,求出N的坐标,求出直线MN的斜率,得到关于t的不等式,求出t的范围即可.
解答 解:(1)过点A作直线AN垂直于直线$y=-\frac{1}{4}$于点N,由题意得|AF|=|AN|,
所以动点A的轨迹是以F为焦点,直线$y=-\frac{1}{4}$为准线的抛物线,
所以抛物线C得方程为x2=y.
(2)由题意知,过点P(t,t2)的直线PQ斜率存在且不为0,设其为k,
则${l_{PQ}}:y-{t^2}=k({x-t})$,当$y=0,x=\frac{{-{t^2}+kt}}{k}$,则$M({\frac{{-{t^2}+kt}}{k},0})$,
联立方程$\left\{\begin{array}{l}y-{t^2}=k({x-t})\\{x^2}=y\end{array}\right.$,整理得:x2-kx+t(k-t)=0.
即(k-t)[x-(k-t)]=0,解得x=t或x=k-t,
∴Q(k-t,(k-t)2),而QN⊥QP,所以直线NQ斜率为$-\frac{1}{k}$,
∴${l_{PQ}}:y-{({k-t})^2}=-\frac{1}{k}[{x-({k-t})}]$,联立方程$\left\{\begin{array}{l}y-{({k-t})^2}=-\frac{1}{k}[{x-({k-t})}]\\{x^2}=y\end{array}\right.$,
整理得:${x^2}+\frac{1}{k}x-\frac{1}{k}({k-t})-{({k-t})^2}=0$,
即kx2+x-(k-t)[k(k-t)+1]=0,[kx+k(k-t)+1][x-(k-t)]=0,
解得$x=-\frac{{k({k-t})+1}}{k}$,或x=k-t.∴$N({-\frac{{k({k-t})+1}}{k},\frac{{{{[{k({k-t})+1}]}^2}}}{k^2}})$,
∴${k_{MN}}=\frac{{\frac{{{{[{k({k-t})+1}]}^2}}}{k^2}}}{{-\frac{{k({k-t})+1}}{k}-\frac{{-{t^2}+kt}}{k}}}=\frac{{{{({{k^2}-kt+1})}^2}}}{{k({{t^2}-{k^2}-1})}}$.
而抛物线在点N的切线斜率,
k=y'|$x=-\frac{{k({k-t})+1}}{k}=\frac{{-2k({k-t})-2}}{k}$,MN是抛物线的切线,
∴$\frac{{{{({{k^2}-kt+1})}^2}}}{{k({{t^2}-{k^2}-1})}}=\frac{{-2k({k-t})-2}}{k}$,整理得k2+kt+1-2t2=0,
∴△=t2-4(1-2t2)≥0,解得$t≤-\frac{2}{3}$(舍去),或$t≥\frac{2}{3}$,
∴${t_{min}}=\frac{2}{3}$.
点评 本题考查了求抛物线的解析式问题,考查求直线的斜率以及转化思想,考查抛物线的性质,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 250 | B. | 300 | C. | 360 | D. | 390 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
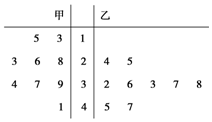 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$,$\overline{x_乙}$;准差分别是s甲,s乙,则有( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,甲、乙两人这几场比赛得分的平均数分别为$\overline{x_甲}$,$\overline{x_乙}$;准差分别是s甲,s乙,则有( )| A. | $\overline{x_甲}$<$\overline{x_乙}$,s甲<s乙 | B. | $\overline{x_甲}$<$\overline{x_乙}$,s甲>s乙 | ||
| C. | $\overline{x_甲}$>$\overline{x_乙}$,s甲<s乙 | D. | $\overline{x_甲}$>$\overline{x_乙}$,s甲>s乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com