
分析 根据向量夹角的余弦公式可求出cosA,进而求出sinA,这样根据三角形面积公式便可得出△ABC的面积.
解答 解:$cosA=\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{xu+yv}{\sqrt{{x}^{2}+{y}^{2}}\sqrt{{u}^{2}+{v}^{2}}}$;
∴$sinA=\sqrt{1-co{s}^{2}A}$=$\sqrt{1-\frac{(xu+yv)^{2}}{({x}^{2}+{y}^{2})({u}^{2}+{v}^{2})}}$=$\frac{|xv-yu|}{\sqrt{{x}^{2}+{y}^{2}}\sqrt{{u}^{2}+{v}^{2}}}$;
∴${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|sinA$=$\frac{1}{2}•\sqrt{{x}^{2}+{y}^{2}}\sqrt{{u}^{2}+{v}^{2}}•\frac{|xv-yu|}{\sqrt{{x}^{2}+{y}^{2}}\sqrt{{u}^{2}+{v}^{2}}}$=$\frac{1}{2}|xv-yu|$.
点评 考查向量数量积的坐标运算,根据向量坐标求向量长度,向量夹角的余弦公式,以及三角形面积公式.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
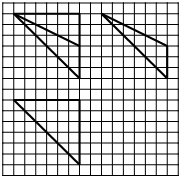 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )| A. | $27\sqrt{2}+9\sqrt{5}+9$ | B. | $27\sqrt{2}+18\sqrt{5}$ | C. | $9\sqrt{2}+9\sqrt{5}+27$ | D. | $36+9\sqrt{5}+18\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
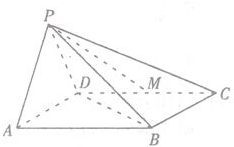 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第8天 | 第16天 | 第22天 |
| 价格(元) | 23 | 24 | 22 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既没有最大值,又没有最小值 | B. | 既有最大值10,又有最小值$\frac{31}{8}$ | ||
| C. | 只有最大值10? | D. | 只有最小值$\frac{31}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,长方体ABCD-A1B1C1D1中,已知AB=BC=2,AA1=1,线段AC1的三个视图所在的直线所成的最小角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,已知AB=BC=2,AA1=1,线段AC1的三个视图所在的直线所成的最小角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com