
分析 (1)利用同角三角函数基本关系式化简所求表达式为正切函数的形式,代入求解即可.
(2)利用诱导公式化简求解即可.
(3)利用三角函数的有界性,结合二次函数化简求解即可.
解答 解:(1)tanθ=-$\frac{3}{4}$,2+sinθcosθ-cos2θ
=$\frac{2si{n}^{2}θ+sinθcosθ+co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$
=$\frac{2ta{n}^{2}θ+tanθ+1}{ta{n}^{2}θ+1}$
=$\frac{\frac{9}{16}-\frac{3}{4}+1}{\frac{9}{16}+1}$
=$\frac{22}{25}$.
(2)f(θ)=$\frac{{2{{cos}^3}θ+{{sin}^2}(2π-θ)+cos(-θ)-3}}{{2+2{{cos}^2}(π+θ)+cos(2π-θ)}}$
=$\frac{2co{s}^{3}θ+si{n}^{2}θ+cosθ-3}{2+2co{s}^{2}θ+cosθ}$
f($\frac{π}{3}$)=$\frac{2co{s}^{3}\frac{π}{3}+si{n}^{2}\frac{π}{3}+cos\frac{π}{3}-3}{2+2co{s}^{2}\frac{π}{3}+cos\frac{π}{3}}$
=$\frac{\frac{1}{4}+\frac{3}{4}+\frac{1}{2}-3}{2+\frac{1}{2}+\frac{1}{2}}$
=$-\frac{1}{2}$.
(3)函数y=cos2x-3cosx+2=(cosx-$\frac{3}{2}$)2-$\frac{1}{4}$≥0,cosx=1表达式取得最小值0.
函数y=cos2x-3cosx+2的最小值:0.
点评 本题考查三角函数化简求值,诱导公式的应用,三角函数的最值,考查计算能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 31 | C. | 30 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [${\frac{1}{2}$,2] | B. | [0,1] | C. | [1,2] | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
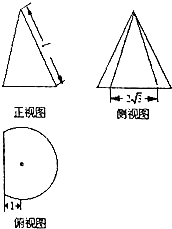 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为2$\sqrt{2}$.
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
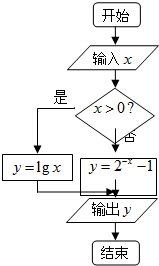 阅读程序框图(如图),完成以下问题:
阅读程序框图(如图),完成以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com