
| A. | [${\frac{1}{2}$,2] | B. | [0,1] | C. | [1,2] | D. | [0,+∞) |
分析 因对任意实数a、b、c,都存在以f(a)、f(b)、f(c)为三边长的三角形,则f(a)+f(b)>f(c)恒成立,将f(x)解析式用分离常数法变形,由均值不等式可得分母的取值范围,整个式子的取值范围由t-1的符号决定,故分为三类讨论,根据函数的单调性求出函数的值域,然后讨论k转化为f(a)+f(b)的最小值与f(c)的最大值的不等式,进而求出实数k 的取值范围.
解答 解:由题意可得f(a)+f(b)>f(c)对于?a,b,c∈R都恒成立,
由于f(x)=$\frac{{{2^x}+t}}{{{2^x}+1}}$=1+$\frac{t-1}{{2}^{x}+1}$,
①当t-1=0,f(x)=1,此时,f(a),f(b),f(c)都为1,构成一个等边三角形的三边长,
满足条件.
②当t-1>0,f(x)在R上是减函数,1<f(a)<1+t-1=t,
同理1<f(b)<t,1<f(c)<t,
由f(a)+f(b)>f(c),可得 2≥t,解得1<t≤2.
③当t-1<0,f(x)在R上是增函数,t<f(a)<1,
同理t<f(b)<1,t<f(c)<1,
由f(a)+f(b)>f(c),可得 2t≥1,解得1>t≥$\frac{1}{2}$.
综上可得,$\frac{1}{2}$≤t≤2,
故实数t的取值范围是[$\frac{1}{2}$,2],
故选A:.
点评 本题主要考查了求参数的取值范围,以及构成三角形的条件和利用函数的单调性求函数的值域,同时考查了分类讨论的思想,属于难题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 无最大值 | |
| B. | 极大值为2 | |
| C. | 极小值为$\frac{2e}{3}$ | |
| D. | 函数g(x)=f(x)-2的图象与x轴只有两个交点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10+5$\sqrt{3}$ | B. | 15 | C. | 10+2$\sqrt{3}$ | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
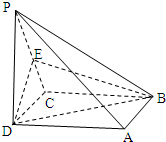 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点,求证:
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com