
���� ��1�������������������Լ����Ǻ��������Ǻ���������Ϊһ���ǵ�һ�����Ǻ�������ʽ�������λ�ķ�Χ���������Һ������н�����⼴�ɣ�
��2���������Һ����ĵ���������⺯���ĵ������䣬Ȼ��������㷨����������ͼ��
���  �⣺��1������f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$����������$\overrightarrow{a}$=��2cos x��1����$\overrightarrow{b}$=��cos x��$\sqrt{3}$sin 2x����
�⣺��1������f��x��=$\overrightarrow{a}$•$\overrightarrow{b}$����������$\overrightarrow{a}$=��2cos x��1����$\overrightarrow{b}$=��cos x��$\sqrt{3}$sin 2x����
��f��x��=2cos2x+$\sqrt{3}$sin 2x
=1+cos 2x+$\sqrt{3}$sin 2x=2sin��2x+$\frac{��}{6}$��+1��
��2sin��2x+$\frac{��}{6}$��+1=1-$\sqrt{3}$��sin��2x+$\frac{��}{6}$��=-$\frac{\sqrt{3}}{2}$��
��-$\frac{��}{3}$��x��$\frac{��}{3}$����-$\frac{��}{2}$��2x+$\frac{��}{6}$��$\frac{5��}{6}$��
��2x+$\frac{��}{6}$=-$\frac{��}{3}$����x=-$\frac{��}{4}$��
��2��-$\frac{��}{2}$+2k��2x+$\frac{��}{6}$��$\frac{��}{2}$+2k��k��Z������-$\frac{��}{3}$+k��x��$\frac{��}{6}$+k��k��Z��
�ú�������������Ϊ[-$\frac{��}{3}$+k�У�$\frac{��}{6}$+k��]��k��Z����
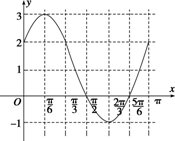
| x | 0 | $\frac{��}{6}$ | $\frac{��}{3}$ | $\frac{��}{2}$ | $\frac{2��}{3}$ | $\frac{5��}{6}$ | �� |
| y | 2 | 3 | 2 | 0 | -1 | 0 | 2 |
���� ���⿼�����Ǻ���������ֵ��������ͼ��Ļ��������Һ����ĵ����Ե����������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{2}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 3+2$\sqrt{2}$ | C�� | 3+$\sqrt{2}$ | D�� | 2+2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [${\frac{1}{2}$��2] | B�� | [0��1] | C�� | [1��2] | D�� | [0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com