
分析 (1)移项通分,化简为整式不等式解之;
(2)利用绝对值的意义去掉绝对值,转化为不等式组解之.
解答 解:(1)$\frac{2x+3}{x-2}$>1变形为$\frac{2x+3}{x-2}-1>0$即$\frac{x+5}{x-2}>0$,等价于(x+5)(x-2)>0,所以不等式的解集为:(-∞,-5)∪(2,+∞).
(2)|2x2-3x+5|≤7,等价于-7≤2x2-3x+5≤7,即$\left\{\begin{array}{l}{2{x}^{2}-3x+5≥-7}\\{2{x}^{2}-3x+5≤7}\end{array}\right.$整理得$\left\{\begin{array}{l}{2{x}^{2}-3x+12≥0}\\{2x{\;}^{2}-3x-2≤0}\end{array}\right.$解得$\left\{\begin{array}{l}{x∈R}\\{-\frac{1}{2}≤x≤2}\end{array}\right.$,所以不等式组的解集为:[$-\frac{1}{2}$,2].
点评 本题考查了分式不等式和绝对值不等式的解法;关键是正确将不等式转化为整式不等式解之.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | 5 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
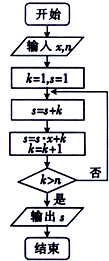 执行如图所示的程序框图.
执行如图所示的程序框图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-4y+15=0 | B. | 4x-3y+6=0 | C. | 4x-3y+6=0或x=3 | D. | 3x-4y+15=0或x=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2,\frac{16}{7})$ | B. | (0,2] | C. | [2,+∞) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com