
分析 利用等差数列的通项公式将已知条件中的不等式化成首项与公差满足的不等关系,利用不等式的性质及等差数列的前n项和公式及线性规划能求出前7项的和的范围.
解答 解:∵等差数列{an}中,-2<a2<2,1<a5<8,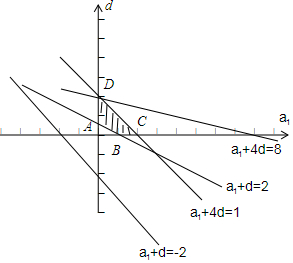
∴$\left\{\begin{array}{l}{-2<{a}_{1}+d<2}\\{1<{a}_{1}+4d<8}\end{array}\right.$,
S7=$\frac{7}{2}({a}_{1}+{a}_{7})$=7(a1+3d)=7a1+21d,
作出可行域四边形ABCD,
得(S7)A=7×$0+21×\frac{1}{4}$=$\frac{21}{4}$,
(S7)B=7×1+21×0=7,
(S7)C=7×2+21×0=14,
(S7)D=7×0+21×2=42.
∴S7的取值范围是($\frac{21}{4}$,42).
故答案为:($\frac{21}{4}$,42).
点评 利用不等式的性质解决问题时,一定要注意不等式的两边同乘以一个负数,不等号要改变方向,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
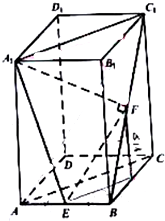 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=a,点E、F分别为AB、C1B的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=a,点E、F分别为AB、C1B的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com