Question

2．如图，在空间几何体ABCDE中，平面ACD⊥平面ABC，△ABC和△ACD都是边长为2的等边三角形，BE=2，点E在平面ABC内的射影落在∠ABC的平分线上，DE∥平面ABC．
（Ⅰ）求直线BE与平面ABC所成的角；
（Ⅱ）求二面角E-BC-A的余弦值．

Answer 1

分析 （I）取AC中点O，连结BO、DO，作EF⊥平面ABC，则垂足F在BO上，∠EBF就是直线BE与平面ABC所成的角，然后求解BE与平面ABC所成的角．
（II）如图建立空间直角坐标系，求出平面EBC的法向量．平面ABC的法向量，利用向量的数量积求解即可．

解答 解：（I）取AC中点O，连结BO、DO，
作EF⊥平面ABC，则垂足F在BO上，∠EBF就是直线BE与平面ABC所成的角，
∵DO⊥AC，平面ACD⊥平面ABC，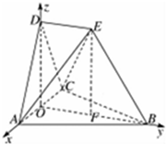

交线是AC，∴DO⊥平面ABC，
则EF∥DO，∴E、F、O、D共面，
∵DE∥平面ABC，面EFOD∩面ABC=OD，
∴DF∥OF，∴$EF=DO=\sqrt{3}$，
∴BE与平面ABC所成的角∠EBF=60°；…（6分）
（II）如图建立空间直角坐标系，则C（-1，0，0），$B（0，\sqrt{3}，0）$，$E（0，\sqrt{3}-1\sqrt{3}）$，
∴$\overrightarrow{CB}=（1，\sqrt{3}，0）$，$\overrightarrow{BE}=（0，-1，\sqrt{3}）$，
设平面EBC的法向量是n=（x，y，z），
由$\overrightarrow{CB}•{n}=0$，$\overrightarrow{BE}•{n}=0$，可取${n}=（-3，\sqrt{3}，1）$
∵平面ABC的法向量是m=（0，0，1），∴$|cos＜{n}，{m}＞|=\frac{{\sqrt{13}}}{13}$，
∵二面角E-BC-A的平面角是直角，∴二面角E-BC-A的余弦值$\frac{{\sqrt{13}}}{13}$．…（12分）

点评 本题考查空间向量的数量积求解二面角的平面角的大小，直线与平面所成角的求法，考查计算能力．