
分析 根据已知中“创新集”的定义,结合韦达定理及反证法,逐一判断四个结论的正误,进而可得答案
解答 解:①∵(3+$\sqrt{3}$)(3-$\sqrt{3}$)=9-3=6=3+$\sqrt{3}$+3-$\sqrt{3}$=6,满足新定义集合;故①是正确的;
②若集合{2,a2}是“创新集”,则2+a2=2a2,解得a=$±\sqrt{2}$;故a=$\sqrt{2}$错误;故②错误;
③若a1,a2∈R,且{a1,a2}是“创新集”,
不妨设a1+a2=a1a2=t,
则由韦达定理知a1,a2是一元二次方程x2-tx+t=0的两个根,
由△>0,可得t<0,或t>4,故②错;
③不妨设A中a1<a2<a3<…<an,
由a1a2…an=a1+a2+…+an<nan,得a1a2…an-1<n,当n=2时,
即有a1<2,
∴a1=1,于是1+a2=a2,a2无解,即不存在满足条件的“创新集”A,故③正确.
当n=3时,a1a2<3,故只能a1=1,a2=2,求得a3=3,于是“创新集”A只有一个,为{1,2,3}.
当n≥4时,由a1a2…an-1≥1×2×3×…×(n-1),即有n>(n-1)!,
也就是说“创新集”A存在的必要条件是n>(n-1)!,事实上,(n-1)!≥(n-1)(n-2)=n2-3n+2=(n-2)2-2+n>2,矛盾,
∴当n≥4时不存在复活集A,故④正确.
故答案为:①③④
点评 本题考查的知识点是元素与集合的关系,正确理解已知中的新定义“创新集”的含义是解答的关键,难度较大.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
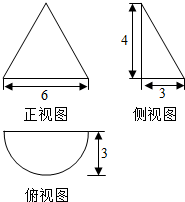
| A. | 12πcm2 | B. | 24πcm2 | C. | (15π+12)cm2 | D. | (12π+12)cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com