Question

【题目】已知函数.

（1）作出函数的图象；

（2）求函数的单调区间，并指出其单调性；

（3）求（）的解的个数.

Answer 1

【答案】（1）详见解析；（2）在，上单调递减，在，上单调递增；（3）当时，有两个解；当时，有三个解；当时，有四个解；当时，有两个解；当时，无解.

【解析】

（1）借助对称性作的图象即可，

（2）由图象写出函数的单调区间即可；

（3）（）的解的个数与图象的交点个数，作出与（）的图象，讨论的位置得到解的个数.

（1）作的图象如下，

，

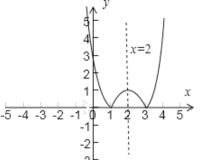（2）由图象可知，在，上单调递减，在，上单调递增；

（3）（）的解的个数与图象的交点个数，

在同一坐标系下作与的图象，易知直线有如下几种位置（虚线部分），

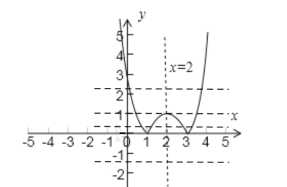
① 当时，与的图象有两个交点，两个解；

② 当时，与的图象有三个交点，三个解；

③ 当时，与的图象有四个交点，四个解；

④ 当时，与的图象有两个交点，两个解；

⑤ 当时，与的图象有无交点，无解；