
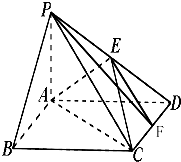
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.分析 (1)欲证EF∥平面PAC,根据直线与平面平行的判定定理可知只需证EF与平面PAC内一直线平行,根据中位线定理可知EF∥PC,PC?平面PAC,EF?平面PAC,满足定理所需条件;
(2)欲证PF⊥AE,而PF?平面PDC,可先证AE⊥平面PDC,根据CD⊥平面PAD,有线面垂直的性质可知AE⊥CD,根据等腰三角形可知AE⊥PD,CD∩PD=D,满足线面垂直的判定定理.
(3)过E坐EM⊥AD垂足为M,过M作MN⊥AC,垂足为N,连接EN.则∠MNE为二面角E-AC-D的平面角,在Rt△MNE中计算即可.
解答 解:(1)证明:当点F为CD的中点时,∵点E,F分别为CD,PD的中点,∴EF∥PC.(3分)
∵PC?平面PAC,EF?平面PAC,
∴EF∥平面PAC.
(2)证明:∵PA⊥平面ABCD,CD?平面ABCD,
∴CD⊥PA.又ABCD是矩形,∴CD⊥AD,
∵PA∩AD=A,∴CD⊥平面PAD.
∵AE?平面PAD,∴AE⊥CD.
∵PA=AD,点F是PD的中点,∴AE⊥PD.又CD∩PD=D,∴AE⊥平面PDC.
∵PF?平面PDC,∴PF⊥AE.
(3)过E坐EM⊥AD垂足为M,过M作MN⊥AC,垂足为N,连接EN.
易证∠MNE为二面角E-AC-D的平面角.
△ACD的边AC上的高为$\frac{1×\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$,∴MN=,$\frac{\sqrt{3}}{4}$,
∵EM=$\frac{1}{2}$,EN=$\sqrt{M{N}^{2}+E{M}^{2}}=\frac{\sqrt{7}}{4}$,
∴cos∠MNE=$\frac{\sqrt{7}}{4}$,
所以二面角E-AC-D的余弦值为$\frac{\sqrt{21}}{7}$.
点评 本题主要考查了直线与平面的判定,以及线面垂直的判定和性质等有关知识,同时考查了空间想象能力和推理论证的能力,二面角等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输出的 ,则判断框内的正整数
,则判断框内的正整数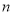 的值为( )
的值为( )
A.7 B.6,7
C.6,7,8 D.8,9
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
要得到函数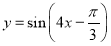 的图像,只需要将函数
的图像,只需要将函数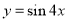 的图像( )
的图像( )
A.向左平移 个单位 B.向右平移
个单位 B.向右平移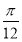 个单位
个单位
C.向左平移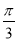 个单位 D.向右平移
个单位 D.向右平移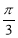 个单位
个单位
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
下列命题中正确的是( )
A.若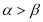 ,则
,则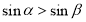 ;
;
B.命题:“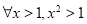 ”的否定是“
”的否定是“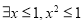 ”;
”;
C.直线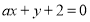 与
与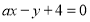 垂直的充要条件为
垂直的充要条件为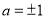 ;
;
D.“若 ,则
,则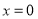 或
或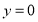 ”的逆否命题为“若
”的逆否命题为“若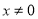 或
或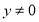 ,则
,则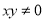 ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
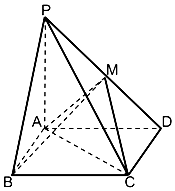 如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.
如图,PA⊥矩形ABCD所在的平面,M,N分别是PC,PA的中点,且PA=AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com